1. горизонтальная плоскость уровня-плоскость, параллельная Н;

2. Фронтальная плоскость уровня - плоскость, параллельная V;

3)Профильная плоскость уровня - плоскость, параллельная w.

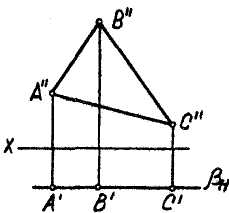
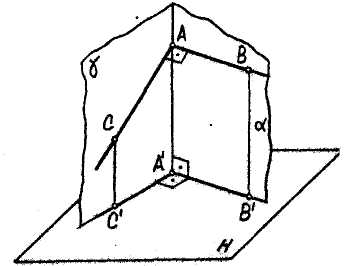
Рис. 3.13

Являясь частным случаем проецирующих плоскостей, плоскости уровня обладают их «собирательным» свойством, так, например, горизонтальная плос­кость уровня является фронтально-проецирующей olLV, поэтому проецируется на плоскость Vв виде своего следа av, параллельного оси х (рис. 3.13, а).

Аналогично, фронтальная плоскость уровня Р перпендикулярна плоскости Я и проецируется на нее в виде следа р н . параллельного оси х (рис. 3.13,6).

3.2.5. Проекции углов, проекция прямого угла

При проецировании величина произвольного угла искажается. Произволь­ный плоский угол проецируется в натуральную величину, если он лежит в плос­кости уровня. Однако известно, что прямой угол проецируется в прямой не только тогда, когда его плоскость параллельна плоскости проекций. Сформулируем и до­кажем теорему.

Теорема. Для того чтобы прямой угол проецировался ортогонально в виде прямого угла, необходимо и достаточно, чтобы по крайней мере, одна его сто­рона была параллельна плоскости проекций, а вторая не перпендикулярна к по­следней.

Допустим, что сторона АВ пря­мого угла ВАС параллельна плоскости Я(рис. 3.14).

Спроецируем угол на Я. При этом лу­чи АА' I Я, ССХН, BB'IH.

Докажем, что угол В'АХ2' - пря-, мой.

По условию теоремы АВ парал­лельна Я. Кроме того, АВ и ее проек­ция А В' лежат в одной проецирующей плоскости а. Из этого следует, что АВ || АЪ'.

Рис. 3.14

Далее известно, что АА' L Н, значит АА' 1АЪ', прямые АВ нАЪ' - парал­лельны, значит АВ 1 АА'.

Таким образом, прямая АВ X АА' и АВ 1 АС, т. е. она перпендикулярна к двум прямым плоскости у, значит она перпендикулярна плоскости у. Но тогда А Ъ' как параллельная АВ, также перпендикулярна плоскости у, а значит она перпен­дикулярна к любой прямой этой плоскости, в частности, ЛВ'А'С- прямой, т. е. теорема доказана.

Применяя полученные выводы к проекциям на комплексном чертеже можно сформулировать такие условия: две взаимно перпендикулярные прямые тогда и только тогда сохраняют перпендикулярность на горизонтальной проекции, когда, по крайней мере, одна из них горизонталь.

Аналогично, эти условия можно записать для фронтальной и профильной проекций (рис. 3.15).

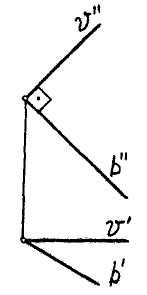
Рис. 3.15

3.2.6. Линии наибольшего наклона

Среди прямых плоскости следует отметить еще замечательные прямые, ксь торые тоже относят к главным - это прямые, образующие с плоскостями проек­ций наибольшие углы. Их называют линиями наибольшего наклона к плоскостям проекций.

Линиями наибольшего наклона называются прямые, принадлежащие плоскости и перпендикулярные к ее линиям уровня.

Линию наибольшего наклона, перпендикулярную к горизонтали, называют также линией наибольшего ската.

С помощью построения этих линий решается задача определения углов на­клона плоскости к плоскостям проекций, т. е. двугранных углов между плоско­стью и плоскостями проекций.

Как известно из стереометрии, двугранный угол измеряется своим линей­ным углом, т. е. углом, образованным прямыми, перпендикулярными к ребру дву­гранного угла. Значит, двугранный угол между плоскостью и плоскостью проекций — это угол между линией наибольшего наклона и ее проекцией на эту плос­кость.

Теорема. Прямые плоскости, перпендикулярные к ее линиям уровня, явля­ются пиниями наибольшего наклона.

В плоскости общего положения р , пересекающей Н по следу р„, проводим пря­мую АВ, перпендикулярную к горизонтали h (ABxh) (рис. 3.16). Необходимо до­казать, что угол наклона прямой АВ к плоскости Я- наибольший но сравнению с углом, образуемым любой другой прямой, например А С.

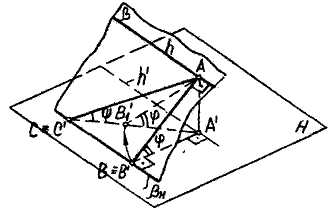
Угол между прямой АВ и плоско­стью Н - это угол между АВ и ее проек­цией на плоскость Н. Проведем А А' перпендикулярно Н, угол АВ'А' = <р -искомый угол.

Докажем, что <р > i|/ - угла между лю­бой другой прямой АС в плоскости (3 и плоскостью Н.

АВ'х Рн, следу плоскости р, так как h |j р_н, а АВ'Х h. Значит А С" больше АВ', так как АВ' - перпендикуляр к рн, а ^Рис-^Зл6 АС- наклонная.

⁴ Рассмотрим два прямоугольных треугольника &.ААЪ'н &АА'С'~ с общим катетом АА'. Вращая &ААЪ'- вокруг АА'до совпадения с аАА'С, совмещаем плоскости рассматриваемых треугольников. Тогда, так как АВ меньше АС, угол ABi'А'=(р больше угла АС'А'= \у - как внешний угол треугольника АС'В/. Итак, доказали, что ср > у, т. е. линия АВ, перпендикулярная к горизонтали, дей­ствительно линия наибольшего наклона к горизонтальной плоскости проекций //. Отметим еще, что проекция линии наибольшего наклона АЪ' X h', и А И' X рн на основании теоремы о проецировании прямого угла, т. е. горизонтальная проекция линии наибольшего наклона к плоскости Н перпендикулярна к горизон-шальной проекции горизонтали.

Аналогичные доказательства можно провести для линий наибольшего на­клона плоскости к плоскостям проекций VhW.

Пример: построить траекторию движения дождевой капли (точки А), скаты­вающейся по плоскости параллельных прямых (а|(Ь)(рис. 3.17).

Построение следует начать с построения горизонтали h(h", h') в плоскости а(а || Ь), Затем, зная, что горизонтальная проекция линии наибольшего ската пер­пендикулярна к горизонтальной проекции горизонтали, строим АЪ' X h', затем по линии связи определяем В" е b", A" e а". Искомая траектория найдена - это AB{AW,A"B").

Для того, чтобы определить угол наклона плоскости а(а \ I b) к плоскости Н, необходимо определить натураль­ную величину отрезка АВ линии ската, построив прямоугольный треугольник на ее горизонтальной проекции АЪ', взяв в качестве второго катета раз­ность высот точек А и В. Искомый угол q> —угол между линией ската А Ъ* и ее горизонтальной проекцией А Ъ'.

Рис. 3.17

3.2.7. Параллельность прямой и плоскости, двух плоскостей

Построение прямой, параллельной данной плоскости основано на известном положении стереометрии: прямая параллельна плоскости, если она параллельна нюбой прямой, лежащей в этой плоскости.

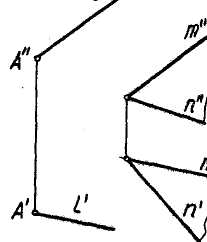
Чтобы построить на эпюре пря­мую /, параллельную плоскости а (тпп) и проходящую через точку А, достаточно построить ее так, чтобы она была параллельна любой прямой, при­надлежащей этой плоскости. Например: /1| т (/' || т', Г || т"). Таких прямых можно построить бесчисленное множество.

Две плоскости параллельны, если две пересекающиеся прямые одной плос­кости соответственно параллельны двум пересекающимся прямым второй плос­кости.

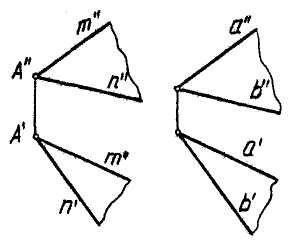
Поэтому, чтобы задать на эпюре плос­кость a (mnn), проходящую через точку А и параллельную плоскости Р (anb), доста­точно построить проекции пересекающихся прямых тип, соответственно параллель­ных прямым а и в (т || а, п || Ъ).

Рис. 3.19