Лекція 7. Метод виправлення наближеної оберненої матриці

Розв’язання СЛР в загальному випадку зводяться до знаходження оберненої матриці коефіцієнтів цих рівнянь. Основні труднощі і виникають саме при обчисленні таких обернених матриць. В багатьох випадках, в особливості в задачах електроенергетики, вдається отримати досить просте грубе наближення оберненої матриці. І якщо його відносно легко виправити, то тоді цей спосіб буде ефективним для розв’язання СЛР.

Розглянемо простий метод виправлення наближеної оберненої матриці. Нехай ми маємо деяку наближену матрицю .

Виправимо цю матрицю методом інерцій. Мірою похибки матриці М, оберненої матриці А є :

Якщо , то

Використаємо послідовне наближення за формулою :

,

де

Швидкість збіжності ітерації на першому кроці :

, а

Тому ,

Відповідно: ,

Коли , то процес ітерації збіжний. Процес ітерації характеризується дуже високою квадратичною швидкістю збіжності. В задачах електроенергетики ми часто маємо справу з матрицями, діагональні елементи яких значно більші за взаємні (наприклад, матриця провідності вузлових напруг, матриця контурних опорів і т.д.). Для таких матриць за нульове наближення оберненої матриці можна прийняти обернену діагональну матрицю з елементами діагоналі оберненої матриці. Потому використовуючи даний метод, можна уточнити обернену матрицю, наближуючи її до дійсної

Приклад

Нехай має матрицю

За нульове наближення приймемо:

– процес ітерації збіжний

Далі:

обернена матриця з точними розрядами

Лекція 8.Розвязання слр методами мінімізації

1.

.

(10.1)

2. Метод найменших квадратів.

Найбільш ефективніший метод для розв’язання недовизначених СЛР (m<n), тобто тобто коли кількість рівнянь менше кількості невідомих. Наприклад:

Така система має безкінечну множину розв’язків. З цієї множини потрібно вибрати якийсь один, який кращий за інших – задовольняє певну критерію. Частіше за все в якості критерія обирають:

Щоб розв'язати СЛР за цим методом не обов'язково шукати min виразу(2). Є раціональніший математичний засіб:

В виразі (1) зробимо заміну:

.

(10.3)

Підставимо (10.3) в (10.1):

.

(10.4)

Вираз (10.4) – нормальна СЛР відносно вектора . З обчислювальної математики відомо, що розв'язок СЛР відносно , а потім підстановка в (10.3) дає вектор , довжина якого буде мінімальною.

Прииклад:

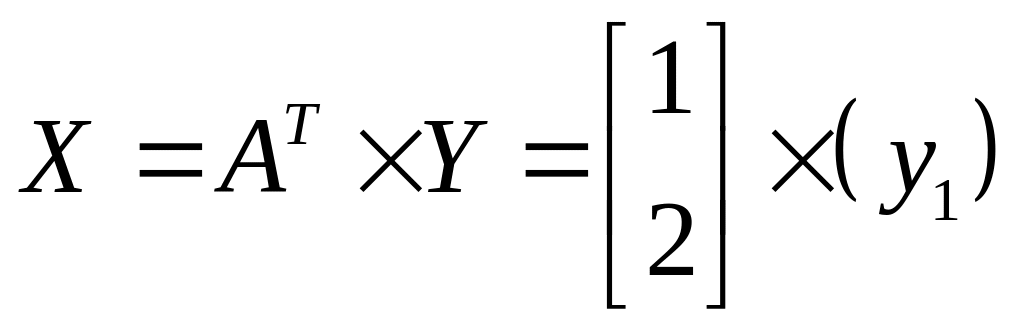
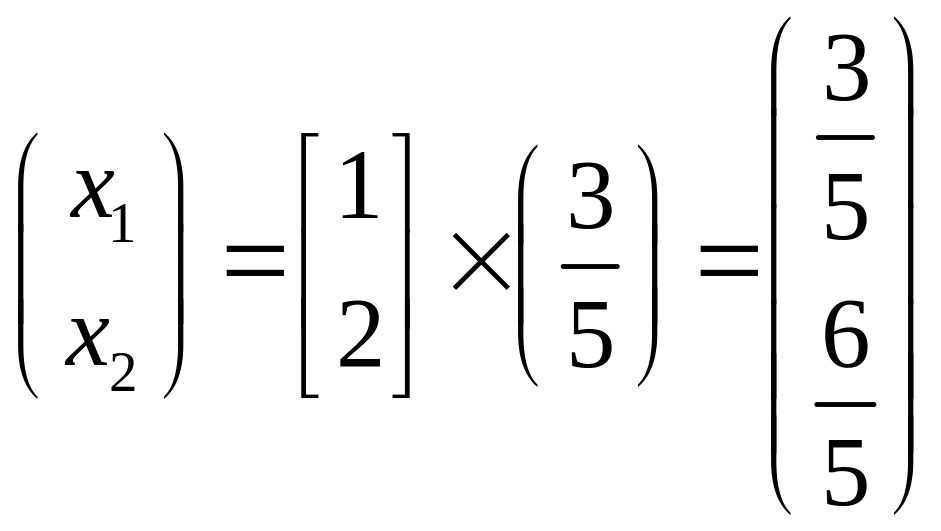
Метод найменших квадратів можна реалізувати і іншим способом – за допомогою розширених матриць, тобто з відомих нам матриць складаються розширені матриці, які утворюють нормальну СЛР:

.

(10.5)

де та – відповідно одинична та нульова матриці заданої розмірності.

Доведемо тотожність (10.5) виразам (10.3) та (10.4). Для цього перемножимо матриці і запишемо їх у вигляді системи:

Вираз (10.5) має ряд переваг.

1) Немає необхідності множити матриці та

2) Вираз (10.5) дає меншу похибку округлення.

3. Метод мінімізації суми квадратів відхилень.

де – i-та строка матриці .

Застосовується для розв’язання перевизначених СЛР, тобто, коли кількість рівнянь більша кількості невідомих ( ).

Наприклад:

Такі системи складаються, коли, наприклад, умов, котрим повинен задовольняти процес, більше ніж параметрів процесу. В загальному випадку ці системи не мають розв’язків. Тоді, вочевидь, нас будуть задовольняти такі розв’язки, які забезпечують оптимальне виконання всіх умов, тобто, дають найменшу похибку .

Для розв’язку (10.1) з використанням критерію в обчислювальній математиці достатньо помножити вираз (10.1) зліва на

.

(10.6)

Вираз (10.6) – це нормальна СЛР,що легко розв’яується будь яким відомим методом

Приклад:

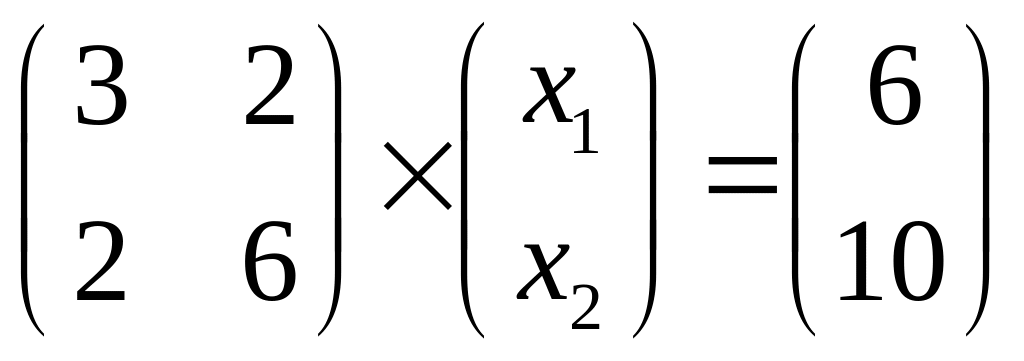
Цей метод також можна реалізувати за допомогою розширених матриць:

.

(10.7)

Доведемо відповідність (10.6) і (10.7)

Застосування розширених матриць має такі ж переваги, що і в попередньому випадку.

Та й до того ж при розв’язанні (10.7) ми одержуємо вектор похибок .