2. Силовые деформации бетона. Деформации бетона при однократном кратковременном загружении.

бетон работает подобно упругому телу только в не­большом диапазоне напряжений или при «мгновенном» (очень быстром) нагружении.

Деформации бетона при однократном кратковременном загружлнии а) Модуль деформаций бетона

Характеристикой упруго-пластических свойств бетона является его модуль деформаций, ус­танавливающий зависимость между напряжениями и относительными деформациями » любой точ­ке диаграммы деформирования (состояния)

Характер диаграммы деформирования «σ-ε» свидетельствует об изменяемости модуля де­формаций

Учитывая нелинейную связь между напряжениями и относительными деформациями обычно при определении модуля продольных деформаций используют

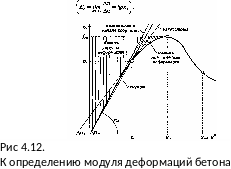- мгновенный (секущий) модуль полных деформаций Е_с, выражаемый тангенсом угла наклона касательной к кривой, описывающей диаграмму «σ-е» , в ее произвольной точке

• модуль упругости Е_ст, выражаемый тангенсом угла наклона секущей, проходящей через начало координат (σ = 0) и точку на кривой при σ = 0,4 fcm

• начальный модуль упругости Е_с0, выражаемый тангенсом угла наклона касательной к кривой, описывающей диаграмму «σ-ε», и проходящей в начале координат σ = 0

б) Значения относительных деформаций в параметрических точках диаграммы дефор­мирования бетона при осевом сжатии

Ес - относительной деформации, соответствующей пиковым напряжениям диаграммы; Еси - предельной относительной деформации бетона при сжатии.

Экспериментальные исследования, выполненные при изучении полных диаграмм деформи­рования показывают, что при изменении класса бетона по прочности при сжатии (даже при одина­ковых начальных технологических условиях) относительные деформации, соответствующие пико­вой точке диаграммы деформирования е_с не остаются величиной постоянной

С ростом прочности бетона на сжатие увеличивается участок упругого деформирования на восходящей ветви диаграм­мы, что обусловливает склонность материала к хрупкому разрушению как в случае высокопрочных бетонов.

Нормы устанавливают значения относительной деформации Ес в зависимости от класса бетона соблюдая установленную тенденцию к ее возрастанию с ростом прочности материала.

2. Деформации бетона при длительном действии нагрузки. Ползучесть бетона.

Опыты показывают, что если сжимающая нагрузка действует на бетонный образец длитель­ное время, его деформация возрастает, стремясь при достаточно продолжительном нагружении (в течение нескольких лет) к некоторому пределу. Такую медленно нарастающую деформацию при неизменном (постоянном) уровне напряжений принято называть ползучестью.

Изменение величины деформаций ползучести зависит от скорости начального нагру­жения. В общем случае величина деформации ползучести бетона зависит от целого ряда факторов, главными из которых принято считать:

• возраст бетона в момент нагружения;

• относительный уровень напряжений, действующих на бетонный образец;

• температура и влажность окружающей среды;

• технологические параметры бетонной смеси

• геометрические размеры поперечного сечения элемента.