29 Расчет изгибаемых элементов тавровой и двутавровой формы сечения
Для решения задач данного типа необходимо обратить внимание на правила назначения эффективной ширины полки beff при расчете тавровых сечений
В зависимости от положения нейтральной оси в сжатой зоне таврового или двутаврового сечения принято рассматривать два расчетных случая:
-
при x
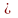hf’
– нейтральная ось пересекает полку;
- при x > hf’ – нейтральная ось располагается вне полки и пересекает ребро таврового или двутаврового сечения.
Для выявления расчетного случая составляют уравнения моментов, либо продольных сил для полки таврового сечения. Для таврового (двутавровго) сечения с одиночным армированием условие, определяющее положение нейтральной оси в сечении, можно записать:
-
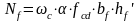упрощенный деформационный метод
Для таврового (двутаврового) сечения с двойным армированием:
-
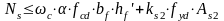упрощенный деформационный метод.
Если условие выполняется, это означает, что нейтральная ось располагается в пределах полки и сечение рассчитывают как прямоугольное.
Если условие не выполняется, производят расчет таврового сечения, для которого равнодействующая усилий в сжатом бетоне определяется по формулам:
-
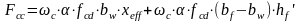упрощенный деформационный метод.
Тогда уравнение моментов относительно центра тяжести площади растянутой арматуры в общем случае можно записать в виде:
-
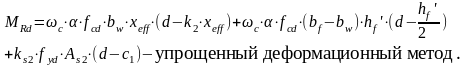При
подборе продольной арматуры положение
нейтральной оси определяется из условия
.
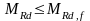Если условие соблюдается – граница
сжатой зоны пересекает полку, если не
соблюдается –ребро.
Момент, воспринимаемый полкой определяется из уравнений:
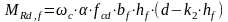-упрощенный
деформационный метод.
Последовательность расчетов железобетонных элементов таврового профиля иллюстрируется в виде блок- схем, приведенных на рис. 8 ...11 и демонстрируется на примерах.
Блок-схема алгоритма расчета площади поперечного сечения продольной арматуры железобетонных элементов таврового профиля при действии изгибающего момента для случая расположения нейтральной оси в полке
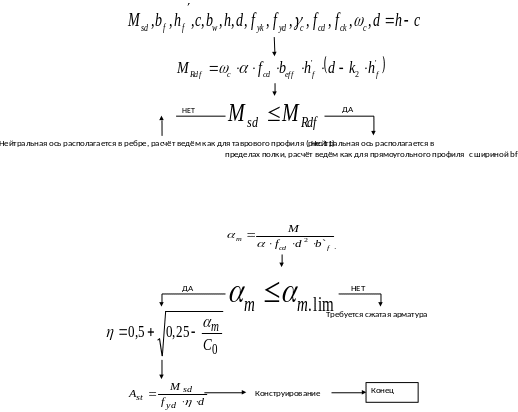
Блок-схема подбора арматуры в тавровом сечении при расположении нейтральной оси в ребре
