Вопрос 7. Ряд распределения. Функции распределения.

Закон распределения может иметь различные формы задания.

Простейшая форма закона распределения – ряд распределения (это таблица, в верхней строке которой перечислены все возможные значения х₁…х_n в порядке их возрастания, а в нижней – соответственно их вероятности(Р₁,Р₂,…,Р_n)).

Пример: в лотерею на каждые 100 билетов разыгрывается 10 выигрышных по 100 рублей, 15 – по 50 рублей и 25 – по 20 рублей.

Построить ряд распределения случайной величины х, обозначающей величину выйгрыша на лотерейный билет.

х₁=0, х₂=20, х₃=50, х₄=100

р₁=(100-10-15-25)/100=0.5, р₂=25/100=1/4, р₃=15/100=0.15, р₄=0.1

х 0 20 50 100

р 0.5 0.25 0.15 0.1

Функция распределения F(x) – вероятность того, что случайная величина х примет значение, меньшее чем заданное х.

Интегральный закон распределения:

F(x)=Р(Х<х)

F(x)=Σ_хi<xР(Х=х_i)=Σ_хi<хрiр_i

Функция распределения ДСВ (дискретной случайной величины) - ступенчатая, разрывная.

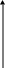
F(x)

1 p_n

P₃

p₂

p₁

x₁ x₂ x₃ x₄ x_n x

Функция распределения – непрерывна слева.

F(x_k-0)=Σ^k-1_i=0P(X=x_i)=F(x_k)

F(x_k=0)=Σ^k_i=0P(X=x_i)=F(x_k)+P(X=x_i)=F(x_k)+P(X=x_k)

F(x_k+0)-F(x_k-0)=P(X=x_k)

1. x≤x₁=0→F(x)=0

2. x₁=0<x≤x₂=20→F(x)=P(X=x₁)=0.5

3. x₂=20<x≤x₃=50→F(x)=P(X=x₁)+P(X=x₂)=0.75

4. x₃=50<x≤x₄=100→F(x)=0.75+0.15=0.9

5. x₄=100<x→F(x)=1

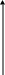F(x)

1

0 .9

0.75

0.5

x₁=0 x₂=20 x₃=50 x₄=100

Для непрерывной – неубывающая кривая.

Основные свойства функции распределения:

1.Функция распределения есть неубывающая функция своего аргумента

х₁<x₂ F(х₁)≤ F(х₂)

2.Предел F(х):lim_x→-∞ F(х)= F(-∞)=0

3.lim_x→∞F(x)= F(∞)=1

Случайная величина – Х – случайная точка на оси х. х – неслучайная величина.

F(x)=P(X<x)

Что означают свойства?

1 .

х₁ х₂

F(x₁) F(x₁)≤ F(x₂)

F(x₂)

2. точка х неограниченно перемещается влево

А≤(Х<х), тогда А становится невозможным, то вероятность его стремится к 0 (и F(x)).

Надо определить попадание случайной величины Х на участок от α до β.

А х< β

В х<α С α≤х< β

α β х

α≤х< β  ХЄ[α;β)

A={X<β}

B={X<α}

A=B+C

C={α≤Х<β}

P(A)=P(B+C)=P(B)+ P(C)

P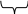 (X<β)=P(X<α)+P(α≤Х<β)

F(β) F(α)

P(α≤Х<β)=F(β)-F(α) (2.2)

P(X=α)=lim_β→αP(α≤Х<β)=lim_β→α[F(β)-F(α)]

HCB:P(X<C)= lim_β→α[F(β)-F(α)]=0

Вопрос 8. Плотность распределения.

F(x) непрерывна и дифференцирована

Р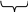 (Х≤a)=P(X<a)+P(X=a)=P(X<a)

0

P(x<X<x+∆x)=F(x+∆x)-F(x)

(2.3.)

f(x)=F^’(x) (2.4)

f(x) – плотность распределения непрерывной случайной величины х

f(x) – дифференциальный закон распределения

f(x)

элемент вероятности = f(x)*dx≈P(x<X<x+dx)

f(x)

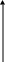f(x) x

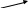P(α<X<β)

x

P(α<X<β)=^β_α∫f(x)dx (2.5)

F(x)=P(X<x)=P(-∞<X<∞)

F(x)=^x_-x∫f(x)dx (2.6)

f(x)

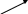F(x)

x

Основные свойства f(x):

1. f(x) – неотрицательная функция (так как F(x) – неубывающая, то ее производная больше либо равна 0 )

2. ^∞_-∞∫ f(x)dx=1 условие нормировки f(x), аналог (2.1) для ДСВ (2.7)