Вопрос 1. События и вероятность.

Событие – всякий факт, который в результате опыта (испытания, эксперимента) может произойти или не произойти.

Таким образом, событие – это исход опыта.

Например: опыт – бросание монеты, событие – выпадение орла или решки.

Вероятность события – численная мера степени объективной возможности этого события. U (достоверное событие) – которое в результате опыта непременно произойдет. V (невозможное событие) – которое не может произойти в результате опыта.

3 Подхода к определению понятия вероятности:

1. классический (подсчет вероятности)

2. статистический (частотный)

3. аксиоматический (теоретико-множественный)

Классический.

Несовместное событие – если появление 1 из них исключает появление других событий в одном и том же опыте.

Полная группа событий: события в опыте образуют полную группу, если в результате опыта произойдет хотя бы 1 из них (например, попадание или промах, орел или решка).

А₁ = {1 или 2 или 3} , А₂ = {3 или 4 или 5}, А₃ = {4 или 5 или 6} – полная группа совместных событий.

Равновозможные события: события в опыте называются равновозможными, если по условиям симметрии есть основания считать, что ни 1 из этих событий не является объективно более возможным, чем другие.

События, обладающие всеми тремя свойствами, называются случаями.

Для каждого опыта можно указать некоторую совокупность взамноисключающих друг друга элементарных исходов. Причем в результате 1 опыта должен осуществится какой-нибудь 1 из них. Эту совокупность и называют совокупностью всех элементарных исходов опыта.

А={1 или 2 или 3}-составное

Если элементарные исходы равновозможные, то это случаи. Тогда опыт сводится к схеме случая. И для таких опытов возможен непосредственный подсчет вероятностей. Он основан на подсчете благоприятных случаев.

Случай является благоприятным событию, если его появление влечет появление данного события.

(1.1)

m(А)-число благоприятных случаев

n-общее число случаев

Р(А)-вероятность события А

Р(А)=3/6 – для игр в кости(четный случай)

1. – только для схемы случая

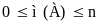2. , следовательно

Р(V)=0

P(U)=1

Пример: в мешке 2 белых и 3 черных шара. Найти вероятность достать белый шара?

А – белый шар

Так как извлекаем наугад, то опыт сводится к схеме случая.

n=5

m(A)=2

P(A)=2/5

Частотный подход основан на понятии частоты. Это опытный подход. Частотой события А в данной серии опытов называем отношением числа опытов, в которых произошло данное событие к общему числу опытов.

(1.3) Р^* (А)=m(А)/n

Р^* - частота А

m(А) – опыты, в которых произошло А

n – число опытов

, следовательно 0≤Р^*≤1

Р^*( V)=0

Р^*( U)=1

Частота имеет свойство устойчивости.

Величина, около которой стремится стабилизироваться частота А при увеличении n называется вероятностью события.

Рассмотрим 2 несовместных события А₁ и А₂. m(А₁ или А₂)=m(А₁)+m(А₂)

Р^*(А₁ или А₂)= m(А₁ или А₂)/n=m(А₁)/ n+m(А₂)/ n= Р^*(А₁)+ Р^*(А₂) (1.6)