1.1. Сравнение эмпирического распределения с теоретическим

В разных задачах подсчет теоретических частот осуществляется по-разному. Рассмотрим примеры задач, иллюстрирующих различ­ные варианты подсчета теоретических частот. Начнем с равноверо­ятного распределения теоретических частот. В задачах такого типа в силу требования равномерности распределения все теоретические частоты должны быть равны между собой.

Задача 1. Предположим, что в эксперименте психологу не­обходимо использовать шестигранный игральный кубик с цифрами на гранях от 1 до 6. Для чистоты эксперимента необходимо получить «идеальный» ку­бик, т.е. такой, чтобы при достаточно большом чис­ле подбрасываний, каждая его грань выпадала бы при­мерно равное число раз. Задача состоит в выяснении того, будет ли данный кубик близок к идеальному?

Решение. Для решения этой задачи, психолог подбрасывал кубик 60 раз, при этом количество выпадений каждой грани (эмпирические частоты ) распре­делилось следующим образом:

Таблица 1.

Грани кубика	1	2	3	4	5	6
-эмпирические частоты	12	9	11	14	8	6
-теоретические частоты	10	10	10	10	10	10

В «идеальном» случае необходимо, чтобы каждая из 6 его гра­ней (теоретические частоты) выпадала бы равное число раз: . Величина и будет, очевидно, теоретической частотой , одинаковой для каждой грани кубика.

Согласно данным подсчитаем величину по формуле:

,

где - эмпирическая частота,

- теоретическая частота,

- количество разрядов признака.

.

Замечание. Для вычисления можно составить таблицу таблица 2.

Таблица 2.

Грани кубика
1
2
3
4
5
6
Суммы			0 !

Теперь, для того чтобы найти , необходимо обратиться к таблице 12 Приложения 1, определив, предварительно число степеней свободы v. В нашем случае (число граней) k = 6, следо­вательно, v = 6 - 1 = 5. По таблице 12 Приложения 1 находим ве­личины для уровней значимости 0,05 и 0,01:

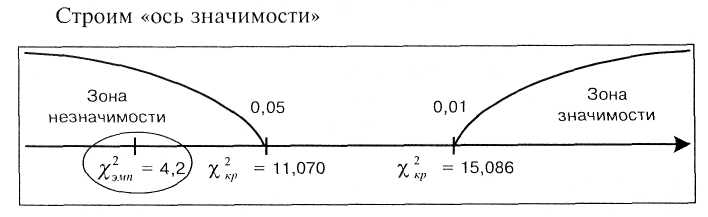
В нашем случае попало в зону незначимости и оказалось равным 4,2, что гораздо меньше 11,070 — критической величи­ны для 5% уровня значимости. Следовательно, можно принимать гипотезу о том, что эмпирическое и теоретическое распреде­ления не различаются между собой. Таким образом, можно ут­верждать, что игральный кубик «безупречен».

Понятно, также, что если бы попало в зону значимос­ти, то следовало бы принять гипотезу о наличии различий и тем самым утверждать, что наш игральный кубик был бы далеко не «безупречен».

При решении приведенной выше задачи с равновероят­ным распределением теоретических частот не было необходимо­сти использовать специальные процедуры их подсчета. Однако на практике чаще возникают задачи, в которых распределение тео­ретических частот не имеет равновероятного характера. В этих случаях для подсчета теоретических частот используются специ­альные формулы или таблицы. Рассмотрим задачу, в которой в качестве теоретического будет использоваться нормальное рас­пределение.

Задача 2. У 267 человек был измерен рост. Вопрос состоит в том, будет ли полученное в этой выборке распределение роста близко к нормальному?

Решение. Измерения проводились с точностью до 0,1 см и все полученные величины роста оказались в диапа­зоне от 156,5 до 183,5 см. Для расчета по критерию целесообразно разбить этот диапазон на интервалы, величину интервала удобнее всего взять равной 3 см, поскольку 183,5 - 156,5 = 27 и 27 делится нацело на 3 . Таким образом, все экспериментальные данные будут распреде­лены по 9 интервалам. При этом центрами интер­валов будут следующие числа: 158, 161, 164, 167, 170,173,176,179,182.

При измерении роста в каждый из этих интервалов попало какое-то количество людей - эта величина для каждого интер­вала и будет эмпирической частотой, обозначаемой в дальней­шем как .

Чтобы применить расчетную формулу , необходимо, прежде всего, вычислить теоретические частоты. Для этого по всем полу­ченным значениям эмпирических частот (по всем выборочным данным) нужно вычислить:

1) среднее .

2) и среднеквадратическое отклонение ( ).

Для наших выборочных данных величина среднего оказа­лась равной 166,22 и среднеквадратическое = 4,06.

Затем для каждого выделенного интервала следует подсчитать величины по формуле (где индекс i изменяется от 1 до 9, т.к. у нас 9 интервалов):

Величины называются нормированными частотами. Удоб­нее производить их расчет с помощью таблицы 3.

Затем по величинам нормированных частот по таблице 11 Приложения 1 находятся величины , которые называются ординатами нормальной кривой для каждой . Величины , полученные из таблицы 11 Приложения 1, заносятся в соответ­ствующую строчку четвертого столбца таблицы 3. Величины, полученные в третьем и четвертом столбцах таблицы 3, позво­ляют вычислить по соответствующей формуле необходимые нам теоретические частоты (обозначаемые как. ) и также занести их в пятый столбец таблицы 3.

Расчет теоретических частот осуществляется для каждого ин­тервала по следующей формуле

,

где n = 267 (общая величина выборки),

= 3 (величина интервала),

— среднеквадратичное отклонение.

Таблица 3.

Центры интервалов	Эмпирические частоты		Ординаты нормальной кривой	Расчетные теоретические частоты
158	3	-2,77	0,0086	1,6
161	9	-2,03	0,0508	10,0
164	31	-1,29	0,1736	34,3
167	71	-0,55	0,3429	67,8
170	82	+0,19	0,3918	77,6
173	46	+0,93	0,2589	51,2
176	19	+1,67	0,0989	19,5
179	5	+2,41	0,0219	4,4
182	1	+3,15	0,0028	0,6
Суммы	267	-	-	267,0

Для вычисления составим таблицу 4, которая получается из таблицы 3, сложением первых двух строк и двух нижних строк, для того, чтобы получить 7 интервалов для упрощения расчетов.

Таблица 4.

Альтернативы
1	12	11,6	+0,4	0,16	0,01
2	31	34,3	-3,3	10,89	0,32
3	71	67,8	+3,2	10,24	0,15
4	82	77,6	+4,4	19,36	0,25
5	46	51,2	-5,2	27,04	0,53
6	19	19,5	-0,5	0,25	0,01
7	6	5,0	+1,0	1,00	0,20
Суммы	267	267	0

В случае оценки равенства эмпирического распределения нормальному, число степеней свободы определяется: . Таким образом, число степеней свободы в на­шем случае будет равно v = 4. По таблице 12 Приложения 1 на­ходим:

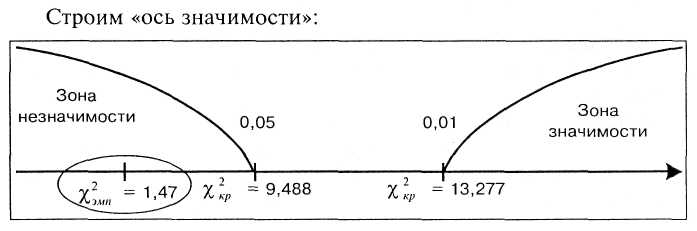
Полученная величина эмпирического значения хи-квадрат попала в зону незначимости, поэтому, необходимо принять ги­потезу об отсутствии различий. Следовательно, существуют все основания утверждать, что наше эмпирическое распределе­ние близко к нормальному.

В заключении подчеркнем, что, несмотря на некоторую «гро­моздкость» вычислительных процедур, этот способ расчета дает наиболее точную оценку совпадения эмпирического и нормаль­ного распределений.