2.6.2. Случай связных выборок

В случае связанных выборок с равным числом измерений в каждой можно использовать более простую формулу t-критерия Стьюдента.

Вычисление значения t_эмп осуществляется по формуле:

где

где - разности между соответствующими значениями переменной X и переменной Y, а среднее этих разностей.

В свою очередь Sd вычисляется по следующей формуле:

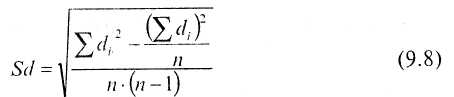
Число степеней свободы к определяется по формуле k = n - 1. Рассмотрим пример использования t - критерия Стьюдента для связных, равных по численности выборок.

Задача 9.2. Психолог предположил, что в результате научения время решения эквивалентных задач «игры в 5» (т.е. имеющих один и тот же алгоритм решения) будет значимо уменьшаться. Для проверки гипо­тезы у восьми испытуемых сравнивалось время решения (в минутах) первой и третьей задач.

Решение. Решение задачи представим в виде таблицы 9.2:

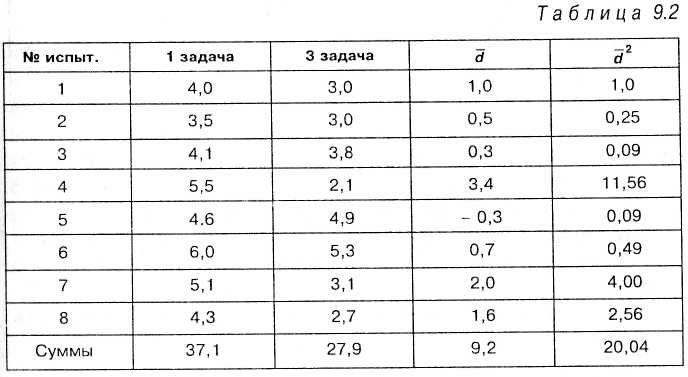
Вначале произведем расчет по формуле (9.7):

Затем применим формулу (9.8), получим:

И, наконец, следует применить формулу (9.6). Получим:

Число степеней свободы: k = 8 – 1 = 7 и по таблице 16 При­ложения 1 находим t_кр :

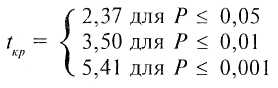
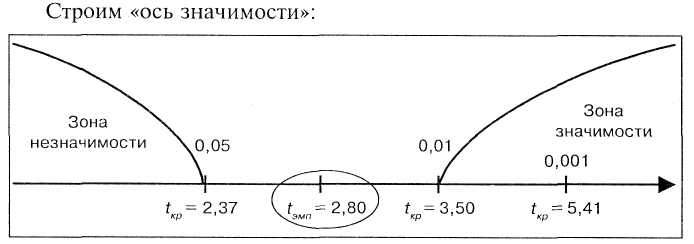
Таким образом, на 5% уровне значимости первоначальное предположение подтвердилось, действительно, среднее вре­мя решения третьей задачи существенно меньше среднего времени решения первой задачи. В терминах статистических гипотез полученный результат будет звучать так: на 5% уров­не гипотеза Н₀ отклоняется и принимается гипотеза Н₁ — о различиях.

Для применения t-критерия Стъюдента необходимо соблюдать следующие условия:

1. Измерение может быть проведено в шкале интервалов и отно­шений.

2. Сравниваемые выборки должны быть распределены по нор­мальному закону.

2.7. F — критерий Фишера

Критерий Фишера позволяет сравнивать величины выбороч­ных дисперсий двух рядов наблюдений. Для вычисления F_эмп нуж­но найти отношение дисперсий двух выборок, причем так, что­бы большая по величине дисперсия находилась бы в числителе, а меньшая знаменателе. Формула вычисления по критерию Фи­шера F такова:

Где

Поскольку, согласно условию критерия, величина числителя должна быть больше или равна величине знаменателя, то значе­ние F_эмп всегда будет больше или равно единице, т.е. F_эмп ≥ 1. Чис­ло степеней свободы определяется также просто: df₁ = п1 - 1 для первой (т.е. для той выборки, величина дисперсии которой боль­ше) и df₂ = п2 - 1 для второй выборки. В таблице 17 Приложе­ния 1 критические значения критерия Фишера F_кp находятся по величинам df_x (верхняя строчка таблицы) и df₂ (левый столбец таблицы).

Задача 9.3. В двух третьих классах проводилось тестирование умственного развития по тесту ТУРМШ десяти учащихся. Полученные значения величин средних достоверно не различались, однако психолога интересует вопрос — есть ли различия в степени однородности показателей умственного развития между классами.

Решение. Для критерия Фишера необходимо сравнить дис­персии тестовых оценок в обоих классах. Резуль­таты тестирования представлены в таблице:

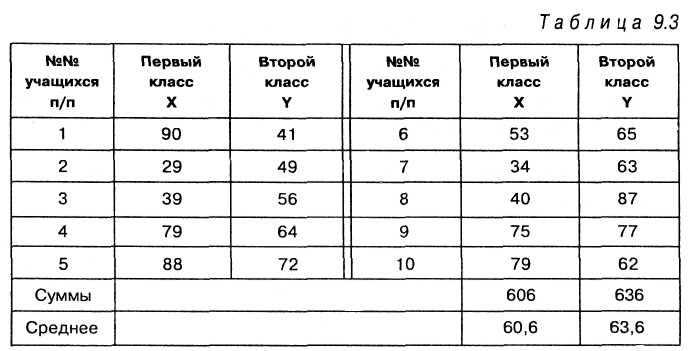
Как видно из таблицы 9.3, величины средних в обеих груп­пах практически совпадают между собой 60,6 ≈ 63,6 и величина t-критерия Стьюдента оказалась равной 0,347 и незначимой.

Рассчитав дисперсии для переменных X и Y, получаем

Тогда по формуле (9.9) для расчета по F критерию Фишера

находим:

По таблице 17 Приложения 1 для F критерия при степенях свободы в обоих случаях равных df = 10 - 1 = 9 находим F_кр .

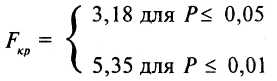
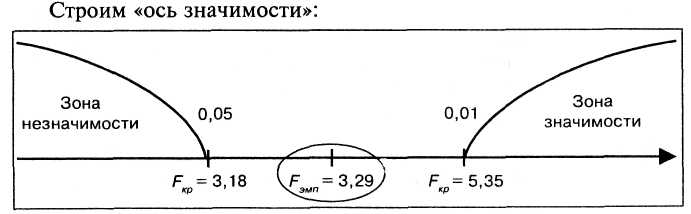
Таким образом, полученная величина F_эмп попала в зону нео­пределенности. В терминах статистических гипотез можно утвер­ждать, что Н_о (гипотеза о сходстве) может быть отвергнута на уровне 5%, а принимается в этом случае гипотеза Н_1. Психолог может утверждать, что по степени однородности такого показа­теля, как умственное развитие, имеется различие между выбор­ками из двух классов.

Для применения критерия F Фишера необходимо соблюдать следующие условия:

1. Измерение может быть проведено в шкале интервалов и отно­шений.

2. Сравниваемые выборки должны быть распределены по нор­мальному закону