15. Гармонический осциллятор. Квантомеханическое описание атома водорода.
Гармоническим
осциллятором называют частицу,
совершающую одномерное движение под
действием квазиупругой силы
.
Потенциальная энергия частицы
где
Гармонический осциллятор в квантовой механике описывается уравнением Шредингера:
Оказалось, что атом водорода – единственный химический объект, для
которого возможно точное решение уравнения Шредингера. Решение для
энергии электрона, входящего в состав этого атома, оказывается функцией
трех
параметров
:
Уравнение Шредингера для атома водорода:
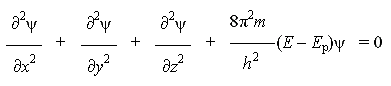
где ψ - волновая функция (аналог амплитуды для волнового движения в классической механике), которая характеризует движение электрона в пространстве как волнообразное возмущение; x, y, z - координаты, m - масса покоя электрона, h - постоянная Планка, E - полная энергия электрона, Ep - потенциальная энергия электрона.
16. Уровни энергии и схема термов щелочных металлов. Дублетная структура спектров щелочных металлов.
Спектры испускания атомов щелочных металлов, подобно спектру водорода, состоят из нескольких серий линий. Наиболее интенсивные из них получили названия: главная, резкая, диффузная и основная (или серия Бергмана). Эти названия имеют следующее происхождение. Главная серия названа так потому, что наблюдается и при поглощении. Следовательно, она соответствует переходам атома в основное состояние. Резкая и диффузная серии состоят соответственно из резких и размытых (диффузных) линий. Серия Бергмана была названа основной (фундаментальной) за свое сходство с сериями водорода.
Еще в конце прошлого столетия Ридберг установил эмпирические формулы, позволяющие вычислить частоты серий щелочных металлов. Эти формулы для всех серий сходны и имеют вид:
где
—частота,
соответствующая границе серии,
—
постоянная Ридберга (59,5),
—целое
число,
—дробное
число.
Таким
образом, частоты линий могут быть
представлены как разности двух термов:
постоянного (
)
и переменного, имеющего более сложный
вид, чем баль-меровский терм
.
Константы
и
а для различных
серий имеют, вообще говоря, разное значение. Так, например, спектральные серии натрия можно представить следующими формулами.
Резкая серия(буква s является начальной буквой наименования серии: sharp — резкий).
Главная серия:(principal — главный),
Диффузная серия:(diffuse — диффузный).
Основная серия (серия Бергмана)(fundamental — основной).:
В соответствии с ростом расщепления уровней при возрастании заряда ядра возрастает и дублетное расщепление спектральных линий, т.е. возрастает рас-стояние между двумя линиями - компонентами дублета.
В настоящей работе изучается дублетная структура линий главной серии в спектрах атомов щелочных металлов (Li, Na, К, Cs) с разным зарядовым числом Z .
Изменение величины дублетного расщепления спектральных линий с возрастанием заряда ядра можно установить, измеряя расстояние между компонентами дублетов главных серий в спектрах щелочных металлов. Для подобных измерений в работе строятся контуры спектральных дублетов указанных элементов. Длины волн этих дублетов приведены в табл. 5.1.
