12. Волновая функция микрочастицы и ее свойства. Стационарное и нестационарное уравнение Шредингера.

Волновая функция имеет статистический смысл: квадрат модуля волновой функции определяет плотность вероятности нахождения частицы в момент времени в области с координатами x и dx, y и dy, z и dz.

Свойства волновой функции:

1) Правило нормировки: правило выражает тот факт, что вероятность обнаружить частицу с данной волновой функцией во всем пространстве равна единице.

2) Импульс частицы в каждом из направлений x, y, z пропорционален первой производной волновой функции, делённой на саму волновую функцию, а именно:

           

где p_x , p_y , p_z — проекции импульсов на соответствующие оси координат, i = √-1 - мнимая единица, ħ = h/2π - постоянная Планка.

3) Кинетическая энергия частицы (p²_x + p²_y + p²_z) / 2m пропорциональна второй производной, или кривизне волновой функции, деленной на эту волновую функцию .

Стационарное уравнение Шредингера для движения электрона в кулоновском поле ядра атома водорода и водородоподобных атомов имеет вид: ∆ψ + (8π²m/h²)(E-U)Ψ = 0,

где Ψ – волновая функция, ∆ - оператор Лапласа, Е – полная энергия электрона в атоме, U = -(Ze²/4πε₀r) – потенциальная энергия.

Домножая стационарное уравнение Шрёдингера на и делая обобщение получаем нестационарное уравнение Шрёдингера:

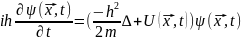
13. Решение уравнения Шредингера для свободной микрочастицы и находящейся в потенциальной яме.

Потенциальная яма – область пространства, где присутствует локальный минимум потенциальной энергии частицы.

Проведем качественный анализ решений уравнения Шредингера применительно к частице, находящейся в потенциальной яме с бесконечно высокими «стенками». Такая яма описывается потенциальной энергией U(x) следующего вида:

где l – ширина ямы, а энергия отсчитывается от ее дна (рис. 5.1).

х

Рис. 5.1

       Уравнение Шредингера для стационарных состояний в случае одномерной задачи запишется в виде:

.

(5.2.1)

       По условию задачи (бесконечно высокие «стенки»), частица не проникает за пределы ямы, поэтому вероятность ее обнаружения за пределами ямы равна нулю. На границах ямы волновая функция также должна обращаться в нуль. Следовательно, граничные условия в таком случае имеют вид:

.

(5.2.2)

В пределах ямы ( ) уравнение Шредингера (5.2.1) сводится к уравнению

(5.2.3)

(5.2.4)

       Общее решение дифференциального уравнения:

.

А т.к. по (5.2.2) , то B = 0. Тогда

,

(5.2.5)

уравнение выполняется только при , где n – целые числа, т.е. необходимо, чтобы

.

(5.2.6)

       Из выражений (5.2.4) и (5.2.6) следует, что энергия частицы зависит от n:

,

(5.2.7)

где n = 1, 2, 3… .

       Т.е. стационарное уравнение Шредингера, описывающее движение частицы в потенциальной яме с бесконечно высокими стенками, удовлетворяется только при собственных значениях E_n, зависящих от целого числа n. Следовательно, энергия E_n частицы в потенциальной яме с бесконечно высокими стенками принимает лишь определенные дискретные значения, т.е. квантуется. Квантовые значения энергии E_n называются уровнями энергии, а число n, определяющее энергетические уровни – главным квантовым числом.

       Таким образом, микрочастица в «потенциальной яме» с бесконечно высокими стенками может находиться только на определенном энергетическом уровне E_n, или, как говорят, частица находится в квантовом состоянии n.