19(1). Основные методы нормализации.

Основные методы нормализации

Существует несколько методов нормализации данных. Рассмотрим ниже четыре из них, которые, с одной стороны, достаточно просты, а с другой — эффективны.

Десятичное масштабирование. Производится путем перемещения десятичной точки на количество цифр в числе, которое определяется исходя из максимального значения признак». 11ри этом преобразование каждого исходного значения признака V(i) в нормализованное значение V ‘(i) производится с помощью выра­жения: V’(i)=v(f)/10^к.

В то же время к выбирается так, что max(V'(i)) < 1.

Минимаксная нормализация. Предположим, что значения некоторого при­знака V лежат в диапазоне от 150 до 250. Предыдущий метод даст все значения нормализованного признака в интервале от 0,15 до 0,25, что не вполне удачно, поскольку они оказываются сконцентрированными в очень небольшом диапа­зоне.

Чтобы получить лучшее распределение значений в пределах интервала [0; 1], можно воспользоваться так называемой минимаксной формулой:

где минимальное и максимальное значения вычисляются автоматически или вы­бираются аналитиком.

Похожее преобразование используется и для нормализации в интервале [— 1; 1]. Хотя поиск минимального и максимального значений в большом множестве дан­ных может занять некоторое время, в целом вычислительная процедура очень проста. Кроме того, выбор минимального и максимального значения аналитиком позволит оптимизировать диапазон, в котором будут распределены нормализован­ные значения с точки зрения решаемой задачи.

Нормализация с помощью стандартного отклонения. Минимаксная нормализация оптимальна, когда значение признака V плотно заполняют определенный интервал. Но подобный подход применим не всегда. Так, если в данных имеются относительно редкие выбросы, намного превышающие типичный разброс, именно они определят согласно предыдущей формуле масштаб нормализации. Это при­ведет к тому, что основная масса значений нормированной переменной V'(i) сосредоточится вблизи нуля: 1. В этом случае гораздо надежнее ориентироваться не на экстремальные значения, а на типичные и использовать для нормализации статистические характеристики данных — среднее и дисперсию. Например, на всем множестве х для некоторого признака V вычисляются среднее значение Vs и стандартное отклонение сигмаv. Затем, для каждого значения признака V'(i) рассчитывается преобразование:

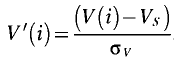
Нормализация с помощью поэлементных преобразований. Еще одним спосо­бом нормализации является поэлементное преобразование членов ряда с помощью различных нелинейных функций, которые способны отображать исходный диапа­зон значений в диапазон, соответствующий параметрам функции преобразования.

Исходный диапазон [v1, v2] преобразуется к более узкому [v1’; v2’].

20(1). Нормализация с помощью поэлементных преобразований.

Нормализация с помощью поэлементных преобразований - Vнов(i)=f(V(i)), где f - такая функция, чтоб интервал значений после преобразования получился уже (или шире), чем до него. В качестве f можно выбирать exp(v), log(v), 1/log(v), v^y или 1/(v^y).

Нормализация с помощью поэлементных преобразований. Еще одним способом нормализации является поэлементное преобразование членов ряда с помощью различных нелинейных функций, которые способны отображать исходный диапазон значений в диапазон, соответствующий параметрам функции преобразования.

Исходный диапазон [v1,v2] преобразуется к более узкому [v1’,v2’].

В данной методике к каждому значению ряда применяется преобразование видаv’=f(v), где v-исходное значение ряда;

v’ -значение после преобразования.