3.3. Базисные решения Представление множества допустимых решений злп в канонической форме

При анализе графического метода решения ЗЛП мы пришли к выводу, что оптимальному решению всегда соответствует одна из вершин множества допустимых решений (либо ребро, грань). Именно этот результат и положен в основу построения метода решения ЗЛП - симплекс-метода. Рассмотрим важные особенности ЗЛП, на которых базируется данный метод, на примере задачи о красках.

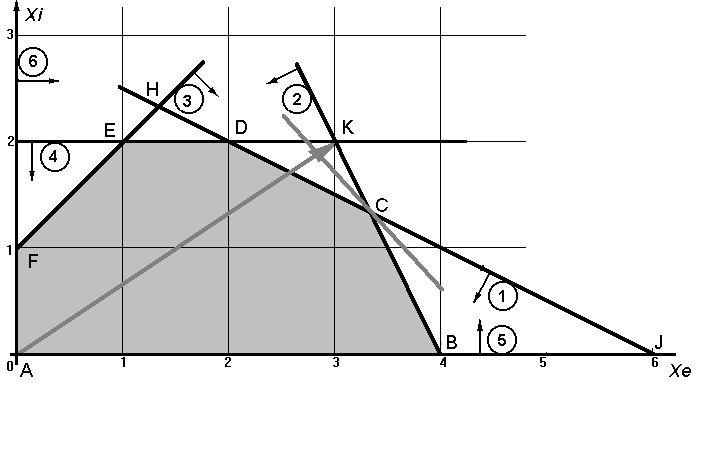
Рис. 4.5

Приведем задачу к канонической форме. Для этого введем в ограничения остаточные переменные . Соответствующая линейная модель, приведенная к канонической форме, имеет вид:

(7)

Рассмотрим множество допустимых решений (МДР) ЗЛП (7): каждую точку этого множества можно определить с помощью переменных x_E, x_I, s₁, s₂, s₃, s₄, фигурирующих в модели канонической формы. Для идентификации нужной точки МДР воспользуемся тем, что при s_i = 0, i = 1,2,3,4 ограничения модели эквивалентны равенствам, которые представляются соответствующими ребрами множества решений. Например при s₁=0 первое ограничение принимает вид равенства x_E + 2x_I = 6, которое представляется ребром СD. Увеличение переменных s_i (s_i>0) будет соответствовать смещению точек с границ МДР в его внутреннюю область.

Рис.

На рисунке видно, что каждой вершине соответствуют две нулевые переменные. Каждая точка внутренней области пространства решений вообще не имеет ни одной нулевой переменной, а каждая точка, лежащая на границе (не вершина), имеет лишь одну нулевую переменную.

Нас, прежде всего, интересует алгебраическое представление вершин многогранника решений. В следующей таблице для каждой вершины определены множества нулевых и ненулевых координат.

Вершина	Переменные
	нулевые	ненулевые
A	xЕ, xI	s1, s2, s3, s4
B	s2 ,xI,	s1, xE, s3, s4
C	s2, s1	xI, xE, s3, s4
D	s4, s1	xI, xE, s3, s2
E	s3, s4	xI, xE, s1, s2
F	s3, xЕ	xI, s4, s1, s2

Анализируя таблицу, легко заметить две закономерности:

• каноническая модель содержит m=4 основных уравнений и n=6 переменных, поэтому в каждой из вершин две (n-m) переменные должны иметь нулевые значения;

• смежные вершины отличаются только одной переменной в каждой группе.

Первая закономерность свидетельствует о возможности определения вершин алгебраическим способом, путем приравнивания нулю n-m переменных (n - количество переменных, m- количество ограничений). То есть, все вершины определяются как все однозначные неотрицательные решения системы m уравнений, в которых n-m переменных равны нулю.

Вторая закономерность оказывается полезной для построения вычислительных процедур симплекс-метода. Так как смежные вершины отличаются только одной переменной, можно определить каждую последующую (смежную) вершину путем замены одной из текущих небазисных (нулевых) переменных текущей базисной переменной.

Чтобы описать рассмотренные процедуры формальными средствами, необходимо определить вершины алгебраически.

Рассмотрим каноническую ЗЛП. [Ляшенко,стр.50-51]

(8) (не вытирать)

Пусть задача имеет допустимые решения и ранг матрицы равен числу ограничений .

Этого можно добиться, исключив из системы линейно зависимые уравнения, что обычно и делается в рамках процедуры предшествующей симплекс-методу.

Кроме того, будем считать, что , т.к. в случае система имеет единственное решение (и, ввиду его единственности, оно является оптимальным).

Если то ранг не может быть равен .

[Пападимитриу, с.33]

Рассмотрим систему ограничений-равенств ЗЛП в векторной форме:

Задачу можно трактовать следующим образом: из всех представлений вектора в виде линейной комбинации векторов с неотрицательными коэффициентами выбрать такое (если оно существует), коэффициенты которого максимизируют значение функции .

def. Базисом ß матрицы А называется набор из линейно независимых столбцов ß .

def. Базисной матрицей называется – матрица, составленная из столбцов, входящих в базис ß:

.

def. Базисным решением, соответствующим базису , называется вектор , в котором

- при

- есть -я компонента вектора , где .

Таким образом, базисное решение можно найти с помощью следующей процедуры.

1. Выбрать множество , состоящее из m линейно независимых столбцов матрицы  .

2. Положить равными 0 все компоненты вектора , соответствующие столбцам, не входящим в ,. Эти переменные будем называть небазисными (их n-m) .

3. Решить полученных уравнений для определения оставшихся компонент вектора . Они будут называться базисными переменными (их m)

def. Решение называется допустимым базисным решением (ДБР), если оно является базисным и все его компоненты неотрицательны.

Если нулевой вектор является допустимым, то его всегда будем считать базисным.

def. ДБР называется невырожденным, если оно имеет точно положительных компонент (координат). Если число положительных компонент меньше , то решение называется вырожденным.

Пример.

Пусть дана система ограничений ( , ).

1. Рассмотрим векторы - они линейно независимы, так как

значит, могут составить базис .

Соответствующая базисная матрица . Соответствующее решение:

допустимое, базисное (ДБР).

2. Рассмотрим векторы - они линейно независимы, так как

значит, могут составить базис .

Соответствующая базисная матрица . Соответствующее решение:

базисное не допустимое решение.

3. Рассмотрим векторы , они линейно-зависимы. Этой системе соответствует бесконечное множество допустимых решений. Одно из них:

допустимо, но не базисное.

4. вырожденное ДБР.

5. Рассмотрим базис вырожденное ДБР

Этому базису соответствует то же решение: .

Итак, так как невырожденное ДБР содержит точно m положительных координат, то его базис всегда единственен. Базис вырожденного решения определен неоднозначно.

На первый взгляд, определение ДБР довольно случайное и не связано с вещами, о которых говорили раньше. Однако это не так.

(8)

Теорема: Вектор тогда и только тогда является допустимым базисным решением задачи (8), когда точка является вершиной его многогранного множества Х.

Доказательство:

В основу доказательства положено определение вершины.

Точка - является вершиной множества Х, если не существует точек таких что , при .

Необходимость Если х – ДБР, то точка х – вершина

Пусть - ДБР задачи (8).

• Если х=0, то этот вектор невозможно представить в виде , где и - допустимые решения, иначе какая-то из компонент одного из этих векторов должна быть отрицательна, т.е. недопустима, что противоречит предположению. Значит - вершина.

• Пусть и первых компонент отличны от нуля, т.е.

(если они не первые , то мы можем их перенумеровать,

отметим, что по определению ДБР).

Доказательство проведем методом от противного.

Предположим, в противоречие с теоремой, что точка не является вершиной многогранного множества , т.е. существуют такие

и

, что

, и , , .

Так как последние координат точки равны нулю, то и последние координат как точки , так и точки должны быть равны нулю (иначе и\или будут недопустимы). Т.о. можно записать:

В виду допустимости точек и имеем

(9)

и

(10)

Вычитая почленно (10) из (9), получим

(11)

Точки и различны, следовательно среди коэффициентов при векторах в (11) есть отличные от нуля, а это означает, что векторы линейно зависимы, что противоречит тому, что – ДБР.

Следовательно, наше предположение неверно и – вершина многогранного множества .

Достаточность: Если точка – вершина, то – ДБР.

Пусть, наоборот, точка – вершина .

Если , тогда – ДБР (по определению).

Пусть и для определенности

(Здесь не зависит от ).

Проведем доказательство от противного.

Предположим, что – допустимое, но небазисное решение. Тогда векторы – линейно зависимы, т.е. существуют такие не все равные нулю, что справедливо:

(12)

Являясь допустимым, вектор удовлетворяет условию

(13)

Умножим обе части равенства (12) на некоторое число :

(14)

Вычтем почленно из уравнения (13) уравнение (14), а затем сложим уравнения (13) и (14)

(13)-(14) (15)

(13)+(14) (16)

Так как , то, всегда, можно найти такое достаточно малое значение множителя , что в равенствах (15) и (16) все коэффициенты при векторах будут неотрицательны. А это означает, что -мерные векторы

и

являются допустимыми и причем различными решениями задачи.

Рассмотрим ВЛК этих точек

Но это противоречит тому, что – вершина . Следовательно не может не быть ДБР.

Итак,

Одна теорема: Если значение ЗЛП конечно, то оптимум - в вершине.

Другая теорема: – ДБР  – вершина,

Из всего этого следует справедливость следующей теоремы.

Теорема (фундаментальная): Если ЗЛП имеет оптимальное решение (в ограниченной области всегда, а в неограниченной – в зависимости от ограниченности целевой функции z), то оно совпадает, по крайней мере, с одним из ДБР системы ограничений.

(Без доказательства).

Эта теорема названа фундаментальной потому, что она указывает на принципиальный путь решения ЗЛП: оптимум следует искать в множестве ДБР.

Теорема. Множество ДБР системы конечно.