Тема 3. Постановка задачи линейного программирования (злп)
1. Формы и терминология злп.
2. Эквивалентность форм злп.
3. Основные свойства и теоремы злп .
1.Формы злп
Задача математического программирования вида:
(1)
(2)
(3)
(4)
(5)
называется задачей линейного программирования (ЗЛП).
Ограничения неотрицательности могут накладываться не на все переменные, т.е. (5) могут иметь вид:
Экономическая интерпретация злп
Определить такие
объемы производства каждого вида
продукции
,
при которых максимизируется доход (1) и
выполняются ограничения, накладываемые
на объёмы использования m
видов ресурсов
(2)-(4). [под ред. Дж.Моудера]
Основными допущениями, принимаемыми при построении линейных моделей, является
1) пропорциональность
2) аддитивность
3) неотрицательность.
Пропорциональность означает, что
затраты ресурсов на некоторый вид продукции прямо пропорциональны его объему выпуска,
вклад этого вида продукции в ЦФ также прямо пропорционален его объему выпуска.
Аддитивность означает, что общая величина ресурса, используемого на производство всех видов продукции, равна сумме затрат этого ресурса на отдельные виды продукции. Аналогично интерпретируется и ЦФ.
Допущения о пропорциональности и аддитивности обеспечивают строгую линейность соответствующих функций.
Неотрицательность в большинстве практических случаев естественна, хотя обусловлена еще и удобствами аналитического представления.
Самостоятельно № 9
Привести примеры, когда эти допущения не выполняются.
В зависимости от вида ограничений различают три основных формы ЗЛП.
ЗЛП вида (1) – (5) называется общей ЗЛП.
ЗЛП вида:
называется стандартной ЗЛП. В матричном виде она записывается следующим образом:
где
,
,
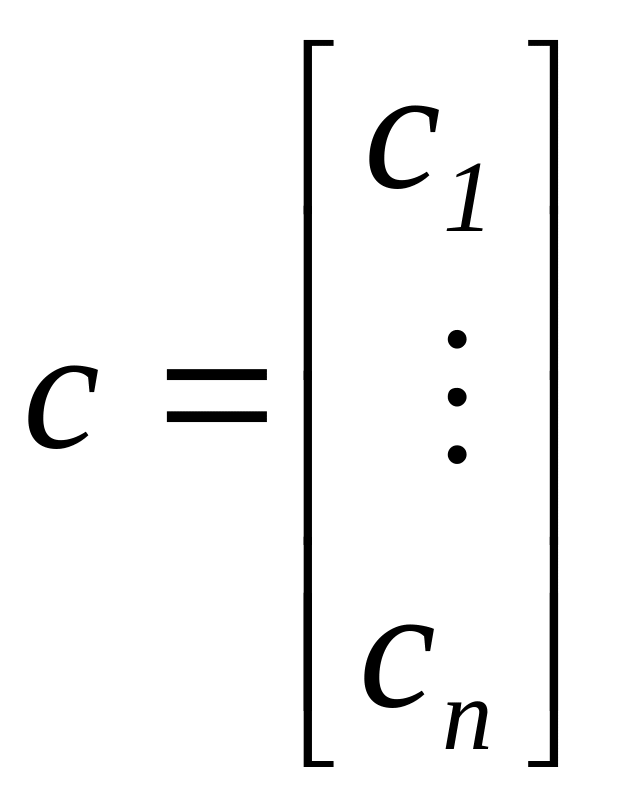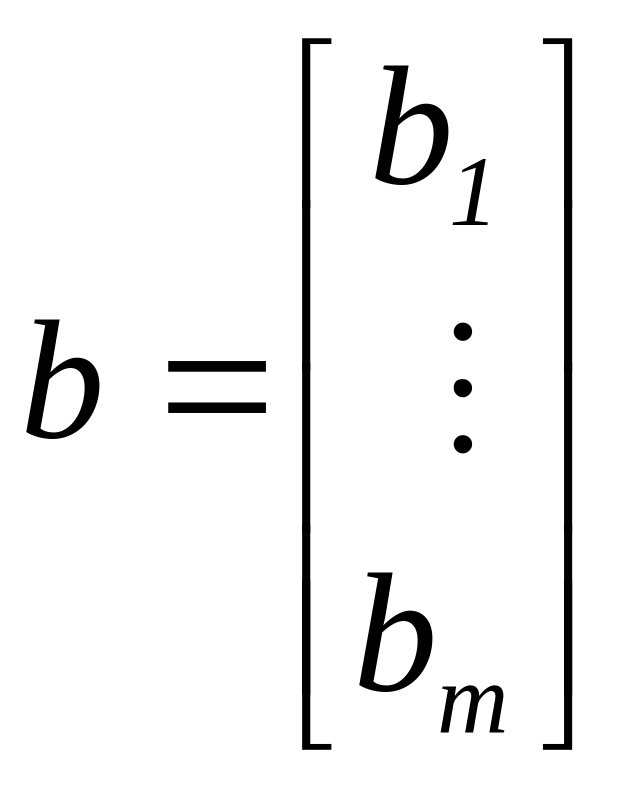ЗЛП вида:
;
;
.
называется канонической ЗЛП.
Она может быть записана в матричном виде следующим образом:
;
Ax=b;
.
Метод решения ЗЛП разработан для задачи в канонической форме.
Далее будем работать с задачей на максимум.
Эквивалентность различных форм злп
Все перечисленные формы ЗЛП являются эквивалентными в том смысле, что простыми преобразованиями задачу, имеющую одну из форм, легко привести к задаче, имеющей одну из оставшихся форм, причем по оптимальному решению построенной задачи легко найти оптимальное решение исходной задачи.
Следовательно, различные формы ЗЛП по существу являются различными формами записи ЗЛП.
Правила преобразования форм ЗЛП
А) Минимизация ЦФ
эквивалентна максимизации ЦФ
.
Б) Ограничение –
неравенство «
»
с помощью введения неотрицательной
переменной
можно заменить на систему:
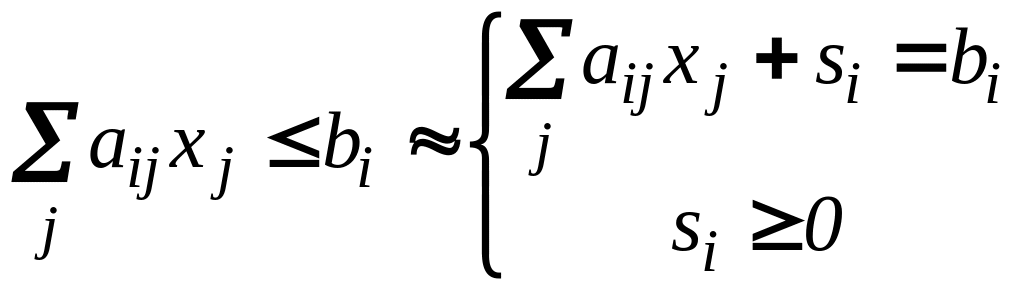
Согласно экономической
интерпретации ЗЛП, исходное ограничение
является ограничением на использование
некоторого ресурса
содержательный смысл переменной
- остаток ресурса. Поэтому переменная
- называется остаточной
переменной.
В) ограничение-неравенство
«
»
с помощью введения неотрицательной
переменной
заменяют на систему.
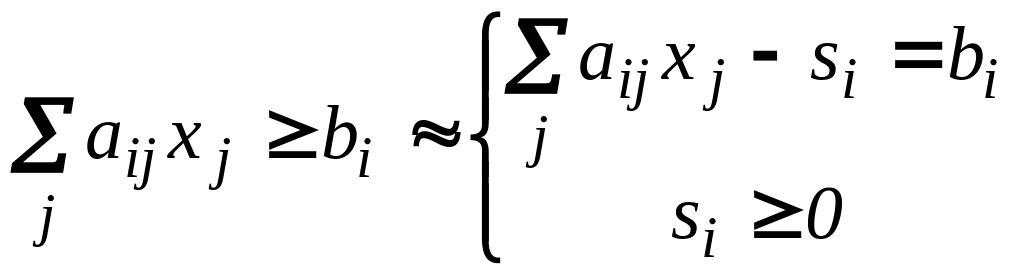
Исходное ограничение можно интерпретировать как некоторые требования к процессу содержательный смысл переменной - величина превышения требований. Поэтому переменная - называется избыточной переменной.
Остаточные и избыточные переменные называются еще свободными, балансовыми, дополнительными.
Г) Ограничение-равенство можно заменить на два неравенства:
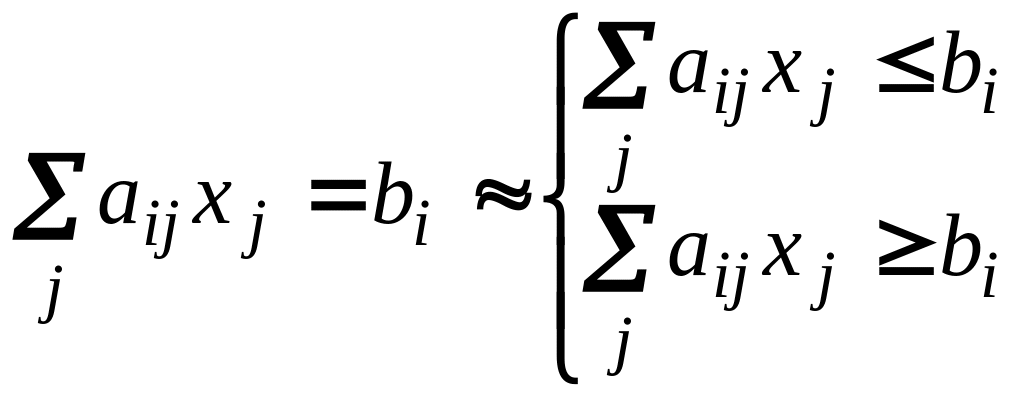
Д) Неравенство « » переводится в неравенство « » умножением его на –1.
Е) m ограничений-равенств можно заменить на (m+1) неравенство:
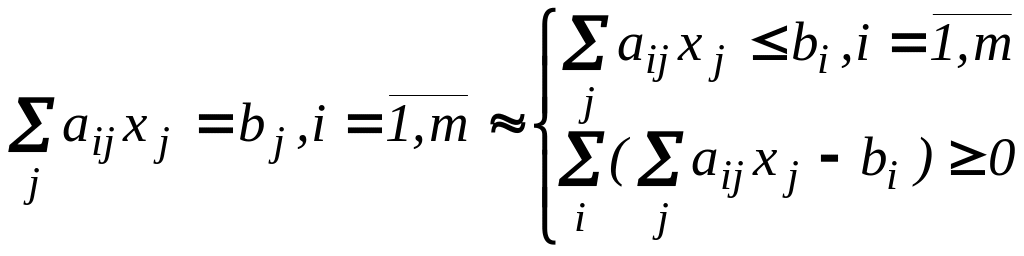
Проанализируем правую систему. Из нее следует m равенств, т.к. в сумме по i каждое слагаемое неположительно, а сумма неотрицательна. Следовательно, это точное равенство.
Ж) Если на
не накладывается ограничения
неотрицательности, то введя новые две
неотрицательные переменные
,
исходную переменную
можно исключить путем замены:
.
Очевидно, всегда найдутся такие
неотрицательные
,
что их разность даст
.
З) Если n
переменных
не имеют ограничений по знаку, то, введя
n+1
неотрицательную переменную
,
исходные переменные можно исключить
путем замены:
(это возможно при условии ограниченности
:
- чтобы можно было подобрать
).
И) Поиск максимума
функции от n переменных можно заменить
на поиск максимального значения одной
переменной
t, введя в ограничения равенство:
.
Пример проведения к канонической форме.
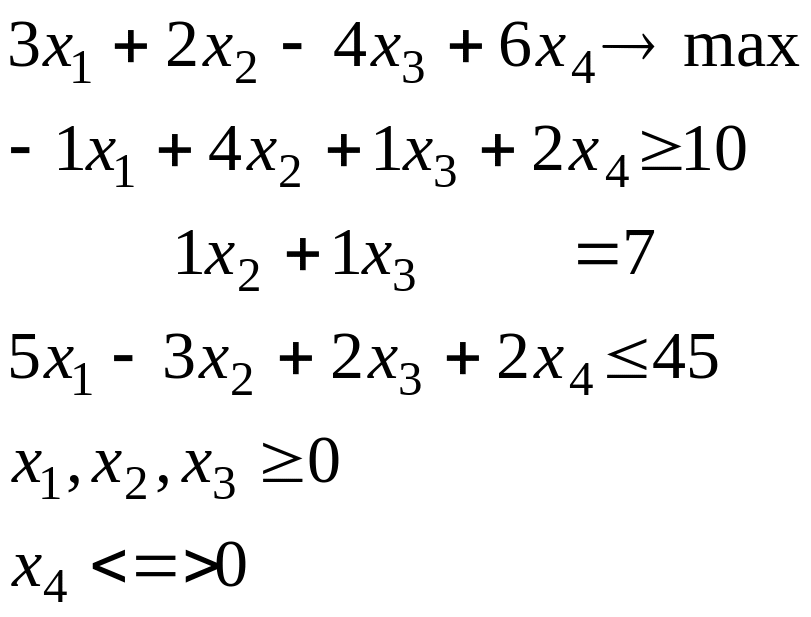
Эквивалентность различных форм ЗЛП рассмотрим на примере стандартной и канонической форм [Ермольев, стр.15 ].
Пусть задана ЗЛП в стандартной форме.
(6)
В матричном виде:
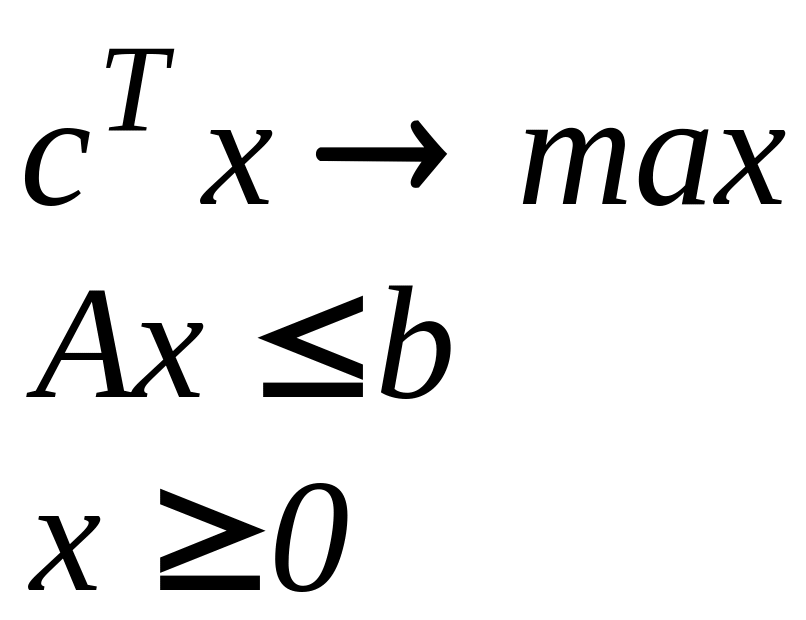(6')
Введем m неотрицательных
переменных
.
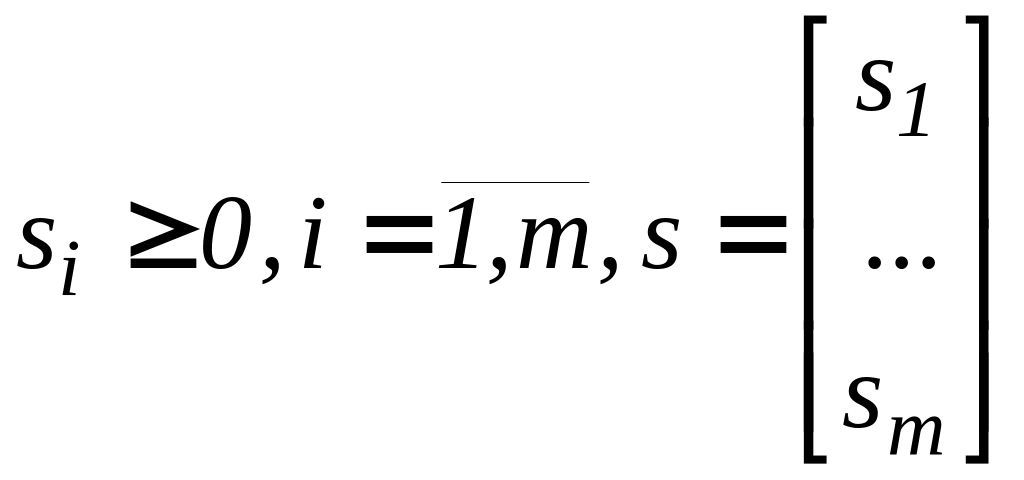Построим с их помощью каноническую ЗЛП:
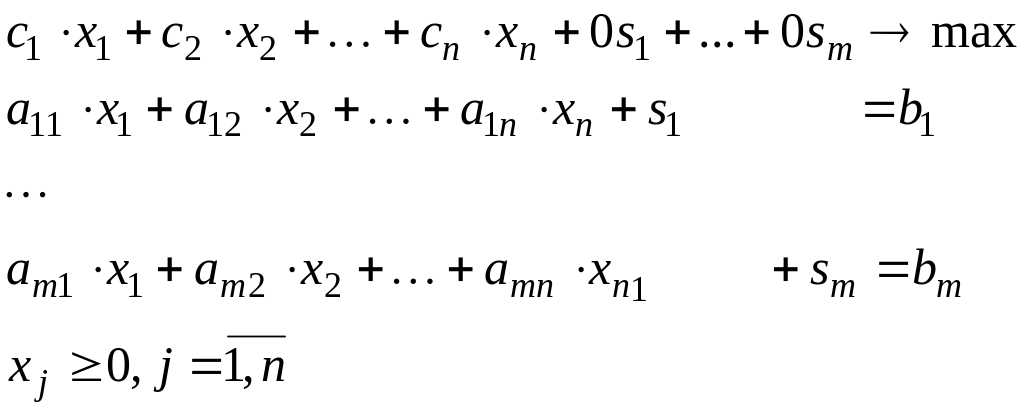(7)
В этой задаче:
вектор переменных
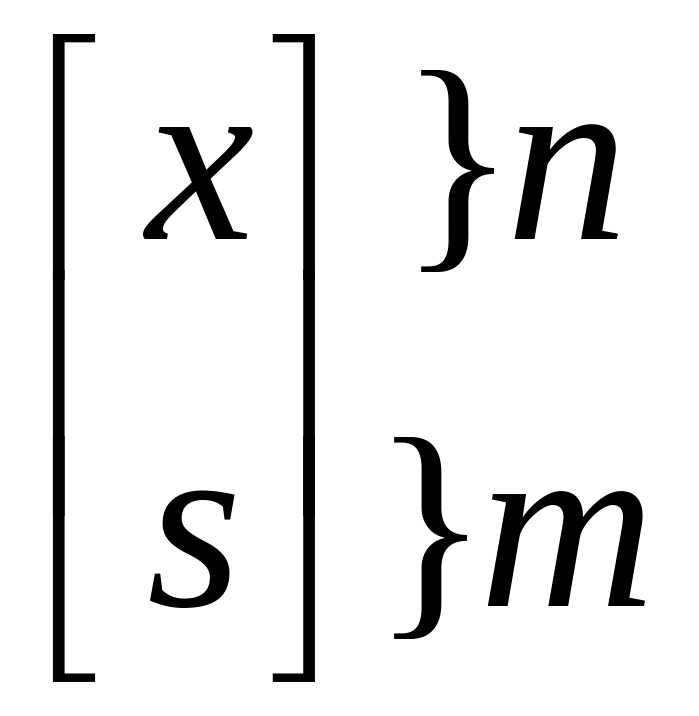
матрица ограничений
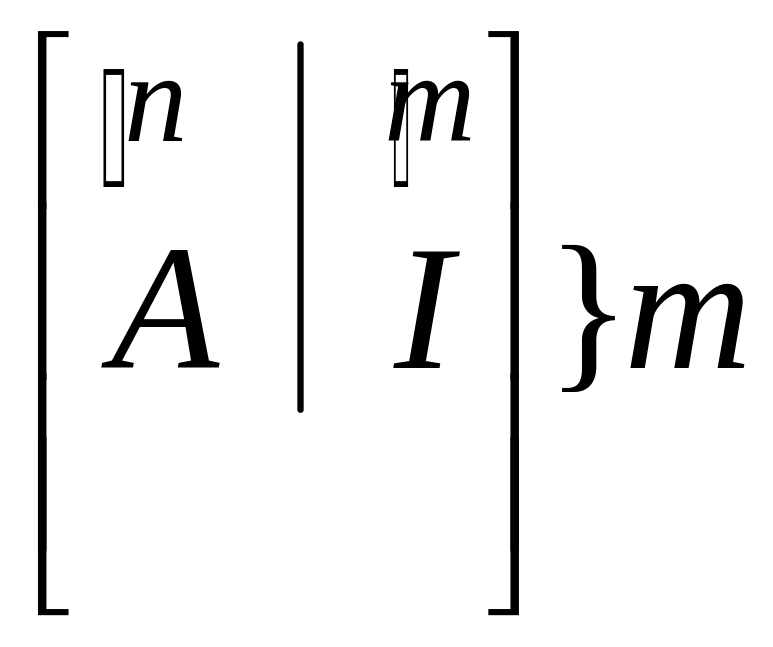
вектор коэффициентов ЦФ
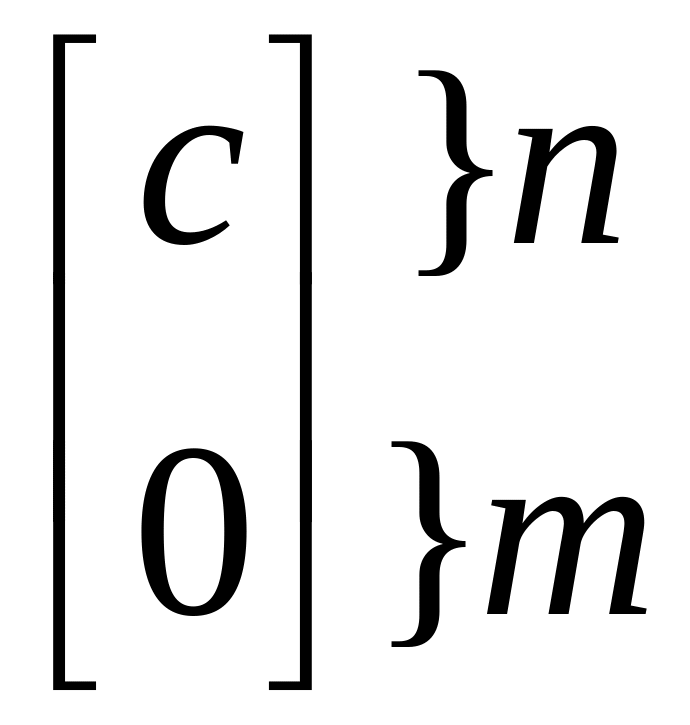
где
– единичная матрица размерности
.
В матричном виде это выглядит так:
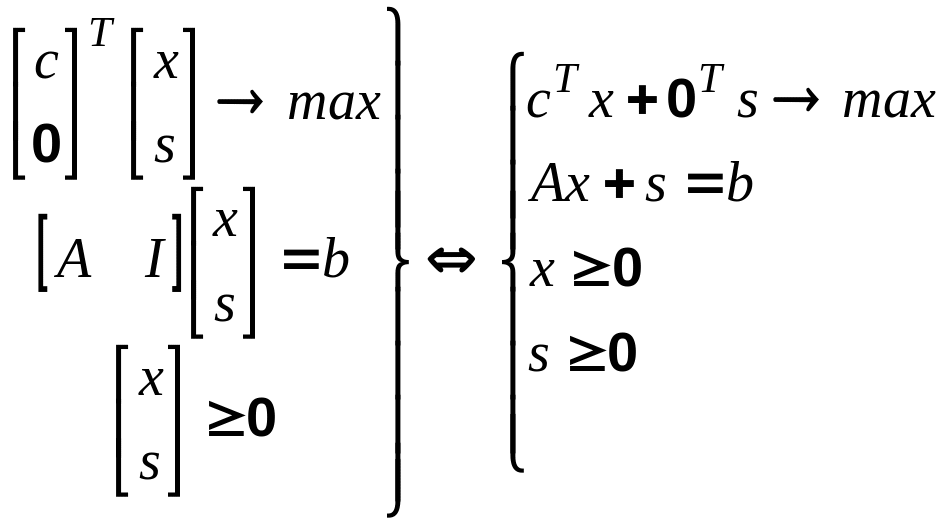(7')
Размерность задачи увеличилась.
Итак, под эквивалентностью форм задач (в нашем случае стандартной и канонической: по решению (допустимому или оптимальному) построенной задачи легко найти решение (допустимое или оптимальное) исходной задачи.
Пусть
-
допустимое решение задачи (6), то есть
,
тогда если мы вычислим вектор
,
(8)
и добавим этот
вектор к вектору
получим вектор
- допустимое решение задачи (7), так как
Таким образом, для
каждого допустимого решения
задачи (6) найдется единственное допустимое
решение
задачи (7), где
определяется соотношением (8).
Очевидно и обратное,
каждое допустимое решение задачи (7)
определяет единственное допустимое
решение
задачи (6) (здесь все значительно проще
– просто отбрасываем подвектор
):
так как из того, что выполняется
(решение
допустимо для (7)), с учетом
имеем
(решение
допустимо
для (6)).
Так как остаточные
переменные
входят в целевую функцию (7) с нулевыми
коэффициентами, то значения
ЦФ задач (6)
и (7) при соответствующих допустимых
решениях одинаковы.
В частности, оптимальному решению задачи
(6) соответствует оптимальное решение
задачи (7) и наоборот.
Итак, путем увеличения размерности задачи ЛП всегда можно перейти к задаче в канонической форме, метод решения которой в дальнейшем и будем изучать.