
- •Билет № 16
- •5.Формула полной вероятности может быть записана как:
- •7. Дисперсия биномиального распределения рассчитывается как:
- •10. Вероятность попадания нормально распределенной св в заданный интервал вычисляется:
- •20. Статистическая гипотеза называется непараметрической, если в ней сформулированы предположения относительно:
- •Билет № 17
- •4. Теорема сложения двух несовместных событий может быть записана как:
- •6. Формула Байеса может быть записана как:
- •Билет № 18
- •Число размещений может быть рассчитано по формуле:
- •6. Случайные величины бывают
- •8. Вероятнейшая частота (наивероятнейшее число) наступления событий рассчитывается как:
- •9. Формула распределения вероятностей Пуассона записывается как:
- •10. Математическое ожидание нсв равно:
- •12. Для расчета коэффициента асимметрии используется:
- •14. Коэффициент вариации рассчитывается:
- •18. Средняя ошибка выборки для доли при бесповторном собственно – случайном отборе может быть найдена как:
- •19. Механическая выборка ориентирована на отбор элементов из генеральной совокупности в выборочную посредством:
- •20. При постановке задачи проверки гипотезы обязательно формулируют н1, которую называют:
- •Задача №2
- •Билет № 19
- •1. Число перестановок может быть рассчитано по формуле:
- •2. Согласно свойству сочетаний:
- •14. Асимметрия характеризует:
- •17. Различают следующие случайные ошибки выборки:
- •18. Необходимый объем выборки для оценки генеральной доли при собственно- случайном бесповторном отборе может быть найден как:
- •19. Серийная выборка базируется на отборе из генеральной совокупности в выборочную
- •Задача №1
- •Задача №2
- •Билет № 20
- •1. Число перестановок с повторениями может быть рассчитано по формуле:
- •Число сочетаний может быть рассчитано по формуле:
- •4. Согласно свойствам вероятности, вытекающим из классического определения, вероятность события находится в интервале:
- •5. Теорема умножения двух независимых событий может быть записана как:
- •7. Формула гипергеометрического закона распределения дсв:
- •8. Вероятность попадания нормально распределенной св в заданный интервал вычисляется:
- •18. Средняя ошибка выборки для доли при бесповторном собственно – случайном отборе может быть найдена как:
- •19. Типическая выборка основана на
- •Задача №2
Билет № 20
1. Число перестановок с повторениями может быть рассчитано по формуле:
А)
|
В)
|
Б)
|
Г)
|
Число сочетаний может быть рассчитано по формуле:
А) С |
В) С ; |
Б) С ; |
Г) С |
3. |
Равновозможные события могут быть определены как: |
А. |
несколько событий называются равновозможными, если в результате опыта наступление одного из них исключает появление других; |
Б. |
несколько событий называются равновозможными, если в результате опыта наступление одного из них не исключает появление других; |
В. |
несколько событий называются равновозможными, если в результате испытания хотя бы одно из них обязательно произойдет; |
Г. |
несколько событий называются равновозможными, если в результате испытания ни одно из них не имеет объективно большую вероятность появления, чем другие. |
4. Согласно свойствам вероятности, вытекающим из классического определения, вероятность события находится в интервале:
А)
|
Б)
|
В)
|
Г)
|
5. Теорема умножения двух независимых событий может быть записана как:
А)
|
В)
|
Б)
|
Г)
|
6. |
Признаками биномиального распределения являются |
А. |
зависимые испытания, дискретная случайная величина, постоянная вероятность наступления события в каждом зависимом испытании; |
Б. |
независимые испытания, непрерывная случайная величина, постоянная вероятность наступления события в каждом независимом испытании; |
В. |
независимые испытания, дискретная случайная величина, постоянная вероятность наступления события в каждом независимом испытании; |
Г. |
зависимые испытания, непрерывная случайная величина, постоянная вероятность наступления события в каждом зависимом испытании . |
7. Формула гипергеометрического закона распределения дсв:
А)
|
Б)
|
В)
|
Г)
|
8. Вероятность попадания нормально распределенной св в заданный интервал вычисляется:
А) ; |
В) ; |
Б) ; |
Г) . |
9. Задача: в ходе аудиторской проверки строительной компании аудитор случайным образом отбирает 5 счетов. При условии, что 10% счетов содержат ошибки, какому закону распределения подчиняется количество счетов с ошибками среди отобранных?
А) биномиальному; |
В) равномерному; |
Б) гипергеометрическому; |
Г) закону распределения Пуассона. |
10. |
Закон больших чисел в “узком смысле” – это |
А. |
совокупность теорем, доказывающих сходимость выборочных характеристик к характеристикам генеральной совокупности при достаточно большом числе наблюдений; |
Б. |
один общий закон, связанный с большими по величине числами; |
В. |
“Золотая теорема” Я. Бернулли; |
Г. |
теорема П.Л. Чебышева. |
11. Относительная плотность - это:
А) отношение частоты интервала к величине интервала; |
В) отношение частости интервала к величине интервала; |
Б) накопленная частость; |
Г) накопленная частота. |
12.
Если значение коэффициента асимметрии
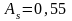 ,
то асимметрия:
,
то асимметрия:
А) существенная левосторонняя; |
В) существенная правосторонняя; |
Б) несущественная левосторонняя; |
Г) несущественная правосторонняя. |
13. Задача: для соревнований из группы выбрано 4 девушки и 3 юноши. Требуется составить волейбольную команду из 5 человек. Какому закону распределения подчиняется количество юношей отобранных в команду?
А) биномиальному; |
В) равномерному; |
Б) гипергеометрическому; |
Г) закону распределения Пуассона. |
14. Вариационные ряды бывают:
А) моментными; |
В) только дискретными; |
Б) только интервальными; |
Г) дискретными или интервальными. |
15. Если все варианты ряда уменьшить в одно и то же число раз k, то дисперсия:
А) не измениться; |
В) уменьшиться в
|
Б)уменьшиться на величину k; |
Г) увеличиться в k раз. |
16. |
Статистическая оценка является состоятельной, если: |
А. |
она удовлетворяет закону “больших чисел”, т.е. сходится по вероятности к оцениваемому параметру; |
Б. |
её математическое ожидание равно оцениваемому параметру генеральной совокупности; |
В. |
ее дисперсия является наименьшей из дисперсий всех возможных оценок заданного объема выборки; |
Г. |
она имеет относительно большую дисперсию. |
17. Если строится 95%-ный доверительный интервал, то в каких границах будет находиться неизвестное значение генеральной средней?
А)
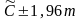 Б)
Б)
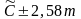
В)
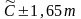

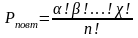 ;
;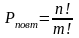 ;
;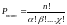 ;
; .
.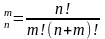 ;
;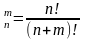 .
.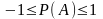
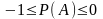
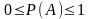
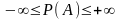
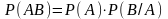
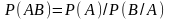
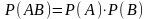
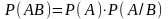
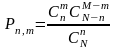 ;
;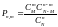 ;
;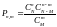 ;
;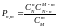 ;
;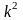 раз;
раз;