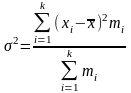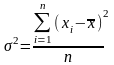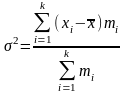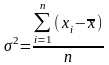14. Асимметрия характеризует:
А) скошенность ряда; |
В) размерность ряда; |
Б) вершинность ряда; |
Г) вариацию ряда. |
15. Формула простой дисперсии записывается как:
А)
|
Б)
|
В)
|
Г)
|
16. |
Доверительная вероятность - это |
А. |
вероятность того, что доверительный интервал накроет неизвестный оцениваемый параметр генеральной совокупности |
Б. |
вероятность, которую можно признать достаточной для суждения о достоверности характеристик, полученных на основе генеральной совокупности |
В. |
вероятность, которая определяется исходя из предположения об обязательном осуществлении события |
Г. |
вероятность суммы двух событий А и В. |
17. Различают следующие случайные ошибки выборки:
А) средняя (стандартная) ошибка; |
В) возможная ошибка; |
Б) предельная ошибка; |
Г) средняя и предельная ошибки. |
18. Необходимый объем выборки для оценки генеральной доли при собственно- случайном бесповторном отборе может быть найден как:
А) ; |
Б) ; |
В) ; |
Г) ; |
19. Серийная выборка базируется на отборе из генеральной совокупности в выборочную
А) целиком некоторых групп элементов, причем попавшие в выборку группы обследуются сплошь; |
В) посредством использования таблиц случайных чисел; |
Б) элементов из списков через определенный интервал; |
Г) при помощи жребия. |
20. |
Какая из данных гипотез является непараметрической: |
А. |
гипотеза о числовом значении доли; |
Б. |
гипотеза о равенстве двух генеральных средних; |
В. |
гипотеза о равенстве двух генеральных дисперсий; |
Г. |
гипотеза о нормальном распределении генеральной совокупности. |
Задача №1
В фирме 550 работников, 380 из них имеют высшее образование, а 412 - среднее специальное образование, 357 сотрудников имеют и высшее и среднее специальное образование. Чему равна вероятность того, что случайно выбранный работник имеет или среднее специальное, или высшее образование, или и то и другое?
Задача №2
Менеджер компании, занимающейся прокатом автомобилей, хочет оценить среднюю величину пробега одного автомобиля в течение месяца. Из 280 автомобилей, принадлежащих компании, методом случайной бесповторной выборки отобрано 30. По данным этой выборки установлено, что средний пробег автомобиля в течение месяца составляет 1342 км со стандартным отклонением 227 км. Считая пробег автомобиля случайной величиной, распределённой по нормальному закону, найти 95%-ный доверительный интервал, оценивающий средний пробег автомобилей всего парка в течение месяца.