19. Механическая выборка ориентирована на отбор элементов из генеральной совокупности в выборочную посредством:
А) использования таблиц случайных чисел; |
В) жребия; |
Б) отбора элементов из списков через определенный интервал; |
Г) использования таблиц случайных чисел или жребия. |
20. При постановке задачи проверки гипотезы обязательно формулируют н1, которую называют:
А) основной гипотезой; |
Б) базовой гипотезой; |
В) альтернативной гипотезой; |
Г) первой гипотезой. |
Задача №1
Вероятность того, что потребитель увидит рекламу определенного продукта по каждому из трех центральных телевизионных каналов, равна 0,05. Предполагается, что эти события - независимы в совокупности. Чему равна вероятность того, что потребитель увидит рекламу: а) по всем трем каналам; б) хотя бы по одному из этих каналов?
Задача №2
Отклонение
стрелки компаса из-за влияния магнитного
поля в определенной области Заполярья
есть случайная величина
.
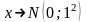Чему равна
вероятность того, что абсолютная величина
отклонения в определенный момент времени
будет больше, чем 2,4?
Билет № 19
1. Число перестановок может быть рассчитано по формуле:
А) Р . |
В)
|
Б) Р |
Г) Р |
;
;
2. Согласно свойству сочетаний:
А)
|
В)
|
Б)
|
Г)
|
;
;
;
;
3. |
Противоположными называются: |
А. |
два единственно возможных и совместных события ; |
Б. |
два равновозможных и совместных события ; |
В. |
два равновозможных и несовместных события ; |
Г. |
два единственно возможных и несовместных события. |
4. |
Классическое определение вероятности гласит: |
А. |
вероятностью события А называют отношение числа исходов, благоприятствующих наступлению этого события, к общему числу всех равновозможных и несовместных событий; |
Б. |
вероятностью события А называют отношение числа исходов, благоприятствующих наступлению этого события, к общему числу всех единственно возможных и равновозможных событий; |
В. |
вероятностью события А называют отношение числа исходов, благоприятствующих наступлению этого события, к общему числу всех единственно возможных, равновозможных и несовместных событий; |
Г. |
вероятностью события А называют отношение числа исходов, благоприятствующих наступлению этого события, к общему числу всех единственно возможных событий. |
5. Теорема сложения двух совместных событий может быть записана как:
А) |
В) |
Б) |
Г) |
6. Вероятность, найденную по формуле Байеса называют:
А) статистической; |
Б) априорной; |
В) апостериорной; |
Г)безусловной. |
7. Формула Бернулли записывается как:
А) ; |
Б) ; |
В) ; |
Г) . |
8. Дисперсия СВ, распределенной по гипергеометрическом закону определяется как:
А)
|
В)
|
Б)
|
Г)
|
;
;
;
.
9. Математическое ожидание СВ, распределенной по закону Пуассона рассчитывается как:
А)
|
Б) ; |
В)
|
Г)
|
;
;
.
10. Нормально распределенная СВ имеет плотность распределения, определяемую формулой:
А)
|
В)
|
Б)
|
Г)
|
;
;
;
;
11. Стандартная (нормированная) нормальная СВ имеет плотность распределения, определяемую формулой:
А)
|
В)
|
Б)
|
Г)
|
;
;
;
.
12. |
В узком смысле слова под законом больших чисел понимают |
А. |
совокупность теорем, в которых устанавливается факт приближения средних характеристик к некоторым постоянным величинам в результате большого числа наблюдений; |
Б. |
центральную предельную теорему Ляпунова; |
В. |
неравенство Маркова; |
Г. |
общий случай теоремы Чебышева. |
13. Задача: вероятность сдать экзамен на право вождения автомобиля одинакова для всех слушателей курсов и равна 0,8. В группе 20 человек. Какому закону распределения будет подчиняться число слушателей, получивших права?
А) биномиальному; |
В) равномерному; |
Б) гипергеометрическому; |
Г) закону распределения Пуассона. |
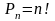
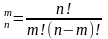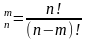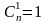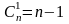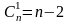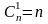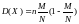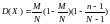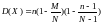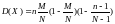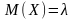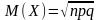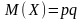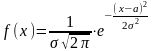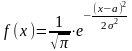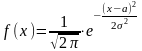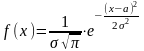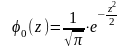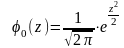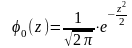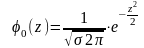