8. Вероятнейшая частота (наивероятнейшее число) наступления событий рассчитывается как:

А) ;

В) ;

Б) ;

Г) .

А) ;

Б) ;

В) ;

Г) .

А) ;

Б) ;

В) ;

Г)

А) биномиальному;

В) равномерному;

Б) гипергеометрическому;

Г) закону распределения Пуассона.

А)центральный момент четвертого порядка;

В) начальный момент четвертого порядка;

Б) центральный момент третьего порядка;

Г) начальный момент третьего порядка.

13.

Полигон – это графическое изображение

А.

интервального вариационного ряда в виде прямоугольников с высотами, пропорциональным частостям или плотностям распределения;

Б.

вариационного ряда с накопленными частотами или частостями по оси ординат;

В.

вариационного ряда с накопленными частотами или частостями по оси абсцисс;

Г.

вариационного ряда в прямоугольной системе координат в виде точек, соединенных отрезками прямой.

А)

Б)

В)

Г)

А) ;

Б) ;

В) ;

Г) .

16

Фундаментальным принципом выборочного метода является:

А.

изучение всех элементов, попавших в выборку;

Б.

случайность отбора элементов из генеральной совокупности в выборочную;

В.

изучение некоторой части элементов, попавших в выборку;

Г.

направленность отбора элементов из генеральной совокупности в выборочную.

17

Статистическая оценка является несмещённой, если:

А.

её дисперсия достаточно велика;

Б.

её математическое ожидание равно оцениваемому параметру генеральной совокупности;

В.

её ожидаемое значение стремится к параметру генеральной совокупности;

Г.

она имеет небольшую дисперсию.

А) ;

Б) ;

В) ;

Г) .
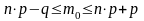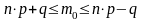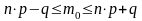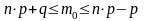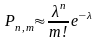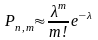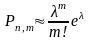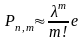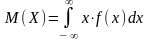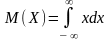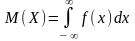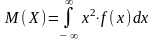
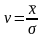
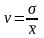
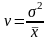
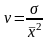
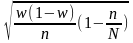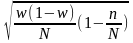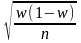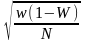