4. Теорема сложения двух несовместных событий может быть записана как:
А)
|
В)
|
Б)
|
Г)
|
5. В коробке 6 красных и 4 зеленых карандаша. Один за другим извлекаются 2 карандаша, не возвращая уже извлеченные. Вероятность того, что оба карандаша будут зелеными может быть найдена как:
А) |
В) |
Б) |
Г) |
;
;
;
.
6. Формула Байеса может быть записана как:
А) |
В)
|
Б)
|
Г)
|
7. |
Случайную величину называют дискретной если: |
А. |
множество ее значений конечно, но несчетно; |
Б. |
она может принять любое значение из некоторого конечного или бесконечного интервала; |
В. |
она может принять конкретное, заранее определенное значение из некоторого конечного или бесконечного интервала; |
Г. |
множество ее значений счетное. |
.
8. Формула Бернулли записывается как:
А)
|
Б)
|
В)
|
Г)
|
;
;
;
.
9. Математическое ожидание СВ, распределенной по гипергеометрическом закону:
А)
|
Б)
|
В)
|
Г) |
;
;
;
.
10. Распределение Пуассона называют также законом распределения:
А) частых событий; |
В) зависимых событий; |
Б) редких событий; |
Г) совместных событий. |
11. Согласно свойствам функции распределения F(x), вероятность того, что НСВ примет одно определенное значение равна::
А)единице; |
Б) нулю; |
В) бесконечности; |
Г) минус бесконечности. |
12. Вероятность заданного отклонения нормально распределенной СВ от ее математического ожидания на величину меньшую Δ равна:
А)
|
В)
|
Б)
|
Г)
|
13. Теорема Чебышева имеет:
А) общий случай; |
В) частный случай; |
Б) классический случай; |
Г) общий и частный случай. |
14. Задача: в барабане книжной лотереи осталось 10 билетов, среди которых 2 выигрышные. Покупатель приобрел 3 билета. Какому закону распределения подчиняется число выигрышных билетов, доставшихся покупателю?
А) биномиальному; |
В) равномерному; |
Б) гипергеометрическому; |
Г) закону распределения Пуассона. |
15. Выбор оптимальной величины интервала для интервального ряда с равными интервалами осуществляется по:
А) абсолютной плотности |
В) формуле Стэрджесса |
Б) относительной плотности |
Г) частости |
16. Средняя арифметическая взвешенная рассчитывается как:
А)
|
Б)
|
В)
|
Г)
|
;
;
;
.
17. |
Оцениваемый параметр может иметь: |
А. |
две точечных оценки |
Б. |
только одну точечную оценку; |
В. |
множество точечных оценок; |
Г. |
три точечных оценки. |
18. Ошибки репрезентативности возникают вследствие:
А) ошибок печати; |
В) искажения сигналов в каналах связи; |
Б) нарушения научных принципов отбора; |
Г) ошибок в вычислении предельной ошибки выборки. |
19. Необходимый объем выборки для оценки генеральной средней при собственно- случайном бесповторном отборе может быть найден как:
А)
|
Б)
|
В)
|
Г)
|
;
;
;
;
20. Критические области бывают:
А) только односторонними; |
В) только трехсторонними; |
Б) только двухсторонними; |
Г)одно- или двухсторонними. |
Задача №1
Фирма нуждается в организации 4 новых складов. Ее сотрудники подобрали 8 подходящих одинаково удобных помещений. Сколько существует способов отбора 4 помещений из 8 в случайном порядке? Какова вероятность того, что в число отобранных попадут 4 помещения, расположенные в многоэтажных зданиях?
Задача №2
В отделе дамской обуви в течение дня проданы туфли размеров: 37, 35, 36, 37, 38, 37, 36, 37, 39, 38, 37, 36, 37, 37, 36. Составьте вариационный ряд. Постройте полигон распределения. Найдите среднюю арифметическую, стандартное отклонение, коэффициент вариации, моду, медиану.
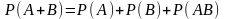
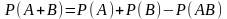
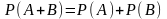
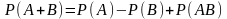
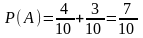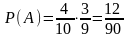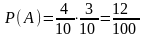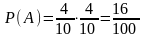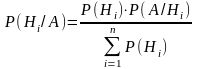
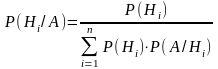
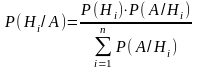
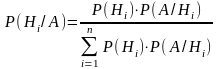
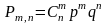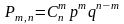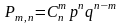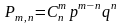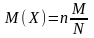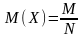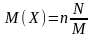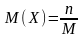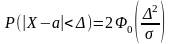
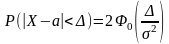
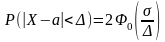
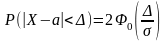
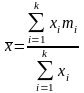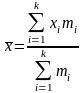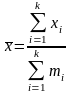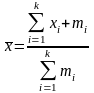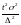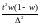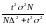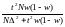