12. Итерационный метод решения обратной кинематической задачи (алгоритм Ньютона). Сущность метода. Управление скоростью сходимости метода.
Среди итерационных алгоритмов наиболее прост и удобен алгоритм Ньютона. Воспользуемся алгоритмом Ньютона второго порядка (алгоритм имеет порядок n, если в нем используются производные функций до (n – 1)-го порядка включительно). Этот алгоритм является компромиссным между двумя важными требованиями к итерационному процессу решения ОЗК в реальном масштабе времени: быстротой сходимости и объемом вычислений. В одномерном случае при решении уравнений f (x) = 0 алгоритм Ньютона второго порядка имеет вид
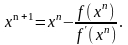(2.22)
Из
(2.22) видно, что для успешного решения
уравнения f(x)
= 0 требуется некоторое «достаточно
хорошее» начальное приближение x0,
такое, чтобы в области xN
– x0,
где xN
– корень уравнения f(x)
= 0, функция f(x)
менялась монотонно (
(x)
0), т. е. xN
– x0
должно быть (при произвольной f(x))
достаточно мало.
Опыт показывает,
что вдоль программной траектории
настолько мало, что вторым слагаемым в
(2.21) можно пренебречь, считая первое
слагаемое главной частью приращения
.
Физически малость вектора
в (2.21) означает малость его в сравнении
с размерами рабочей зоны ИМ X.
Рассмотрим алгоритм
Ньютона для решения ОЗК. Пусть
заданное значение технологических
координат;
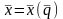
ПЗК;
ошибка при итерации. Найдем корни
системы уравнений
= 0. По условию
.
Пусть
некоторое приближение к корням;
.
Получим следующий алгоритм:
.
(2.23)
Данный способ построения алгоритма Ньютона имеет следующие технические недостатки (при максимально возможной динамической точности решения ОЗК):
сложность переключения на управление положением в обобщенных координатах;
интервал дискретизации при решении ОЗК должен быть мал и равен интервалу дискретизации при расчете системы управления скоростью ИМ.
14. Принцип действия силомоментных датчиков.
Датчики, регистрирующие изменение динамических соотношений в сочленениях исполнительного механизма при их взаимном перемещении, а также динамические напря-жения в теле манипулятора включим в состав силомоментной информационной системы.
Структурно СМД представляет собой многоканальную измерительную систему в виде совокупности упругих и чувствительных элементов, специальным образом ориентированных в пространстве. Процедура преобразования информации в СМД заключается в получении вектора электрических сигна-лов U, компоненты которого пропорциональны компонентам главного вектора сил и мо-ментов F. Следовательно, функцию преобразования СМД можно описать выражением: U = S F, где S - матрица чувствительности.
Наиболее распространенными измерителями деформаций являются ТР, а также пьезо- и магнитострикционные преобразователи, измерителями перемещений - оптронные пары или электромагнитные (реже - электростатические) ЧЭ.