29. Определение средней (расходной) скорости при движении ламинарного потока в трубе
При ламинарном течении максимальная скорость находится на оси трубы. У стенок трубы скорость равна нулю, т.к. частицы жидкости покрывают внутреннюю поверхность трубопровода тонким неподвижным слоем. От стенок трубы к ее оси скорости нарастают плавно. График распределения скоростей по поперечному сечению потока представляет собой параболоид вращения, а сечение параболоида осевой плоскостью - квадратичную параболу.
Уравнение, связывающее переменные υ и r, имеет следующий вид: , где P1 и P2 - давления соответственно в сечениях 1 и 2. , Р1-Р2=hтр (потери давления на трение), µ - динамическая вязкость жидкости, R - радиус трубы, r - текущий радиус.
У стенок трубы υ = 0, а при r = 0 (на оси потока) скорость будет максимальной
Расход :
Если вместо R подставить диаметр трубы d, то (формула Пуазейля) или .
Расход в трубе можно выразить через среднюю скорость:
откуда .
30. Вывод формулы Дарси-Вейсбаха
Преобразуем формулу Пуазейля выразив расход Q через произведение средней
скорости
и площади поперечного сечения
для
удобства преобразуем ее
учитывая,
что
, получим
Обозначая
через
,
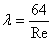получим окончательно, что потери по
длине
----
формула Дарси-Вейсбаха.
31. Профиль скоростей при турбулентном движении жидкости в круглой трубе. Ламинарный пограничный слой
П
ри
турбулентном режиме движения жидкости
в трубах эпюра распределения скоростей
имеет вид, показанный на рис. 4.6. В тонком
пристенном слое толщиной δ жидкость
течет в ламинарном режиме, а остальные
слои текут в турбулентном режиме, и
называются турбулентным
ядром.
Таким образом, строго говоря, турбулентного
движения в чистом виде не существует.
Оно сопровождается ламинарным движением
у стенок, хотя слой δ с ламинарным режимом
весьма мал по сравнению с турбулентным
ядром.
32. Понятие о шероховатости стенок трубы и режиме «гидравлически гладких» труб
Шероховатость поверхности труб может быть весьма различной. Если поверхность труб покрывается специально отсортированными зернами песка одной фракции, то получается равнозернистая шероховатость. Она используется только в лабораторных исследованиях.
Поверхность труб обычно неравнозернистая, она может быть волнистой с различными высотами и длинами волн (или микроволн).
Шероховатость стенок труб определяется рядом факторов: материалом стенок, характером механической обработки внутренней поверхности трубы, наличием или отсутствием в трубе ржавчины, коррозии, отложения осадков, защитных покрытий и т.д.
Для грубой количественной оценки шероховатости вводится понятие о средней высоте выступов шероховатости. Эту высоту, измеряемую в линейных единицах, называют абсолютной шероховатостью . Опыты показали, что при одной и той же величине абсолютной шероховатости влияние ее на величину гидравлических сопротивлений и распределение скоростей различно в зависимости от диаметра трубы. Поэтому вводится понятие об относительной шероховатости, измеряемой отношением абсолютной шероховатости к диаметру трубы, то есть величиной / d.
Понятие о гидравлически гладких и гидравлически шероховатых трубах.
Если высота выступов шероховатости меньше, чем толщина вязкого подслоя в, то все неровности полностью погружены в этот подслой и жидкость в пределах этого подслоя плавно обтекает выступы шероховатости. В этом случае шероховатость стенок не влияет на характер движения и, соответственно, потери напора не зависят от шероховатости. Такие стенки и трубы условно называются гидравлически гладкими.
Если высота выступов шероховатости превышает толщину вязкого подслоя в, то неровности стенок выходят в пределы турбулентного ядра, поток обтекает выступы с отрывом, сопровождающимся интенсивным перемешиванием частиц. В этом случае потери напора зависят от шероховатости, и такие трубы называются гидравлически шероховатыми.
В третьем случае, являющемся промежуточным между двумя вышеуказанными, абсолютная высота выступов шероховатости примерно равна толщине вязкого подслоя.
Толщина
вязкого подслоя определяется как:
.
Таким образом, с ростом числа Re,
а также коэффициента Дарси ,
толщина вязкого подслоя в
уменьшается.