1. Паліномы ад адной літары: азначэнне, аперацыі з паліномамі. Ступень палінома. Ступень сумы і здабытку паліномаў.
АЗН:
Няхай К – гэта камутатыўнае кольца з
адзінкай, х – сімвал, які
мн-ву
К. Тады
,
паліном ад адной літары. (
).
– каэфіцыенты
палінома,
– вольны складнік. Калі
складнік
– старшы складнік,
– старшы каэфіцыент, n
– ступень палінома. (n=deg
f(x))
Прыклад:
1)
,
2= deg
f(x),
2)
,
2= deg
f(x),
3)
– нулявы паліном, deg
f(x)=-
,
К[х] – мноства ўсіх паліномаў ад літары х з кардынатамі з кольца К.
АЗН:
Няхай дадзена 2 паліномы
.
Будзем гаварыць, што паліном
,
калі выконваюцца наступныя ўмовы:
1.
m=n,
і=
2.
m>n,
,
,
і=
3.
m<n,
,
,
і=
АЗН:
Няхай дадзена 2 паліномы
.
Тады суммай паліномаў
,
мы будзем называць h(x)=
h(x)=
,
дзе
,
,
k=max{m,n}.
Прыклад:
f(x)=
,
g(x)=
,
n(x)=
АЗН:
Няхай дадзены паліномы
.
Тады
.
Прыклад:
f(x)=
,
g(x)=
,
k=2
,
,
,
СТВ:
Калі
у кольцы К няма дзельнікаў 0 і паліномы
f(x)
і g(x)
[x],
то тады ступень здабытку паліному
deg
=
deg
f(x)+ deg g(x)
2. Кольца паліномаў ад 1-ой літары над полем.
Тэарэма:
Мноства
[x]
з аперацыямі
і
- гэта каммутатыўнае кольца з 1-й.
1) ( [x], ) – абелева гр.
- складанне на мн-ве [x] – бінарная алгебраічная аперацыя {па азнач. склад. паліномаў}
-
f(x)
(g(x)
h(x))
= (f(x)
g(x))
h(x)
{гэта вынікае з азнач. складання паліномаў.
Пры складанні паліномаў складваюцца
іх каэф., якія з’яшляюцца элементамі
кальца К. А ў кальцы К складане – гэта
ассац. аперацыя.}
-
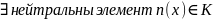[x]
:
{
}
-
.
{
}
-
.
{Гэта
вынікае з азн. склад. палінома і з таго,
што складанне у кольцы К каммут. аперацыя.}
2) Множанне каммутатыўная аперацыя
(f(x) g(x)) h(x) = f(x) (g(x) h(x)) .
{Пры
множанні паліному мы можым складнікі
выгляду
,
прыводзім падобныя. Таму, каб даказаць
ассац. множання, нам дастаткова дак.
ассац. мн-ня для складнікаў
выгляду:
;
;
,
правая ч-та:
=
правая
ч-ка=левай}
3)
Дыстрыбутыўнасць
множання
і
.
{
.
левая ч-ка:
,
правая ч-ка:
правая
ч-ка=левай}
з
1), 2), 3) мн.
з аперац.
і
- кольца.
4)
Пакажам, что
каммутатыўнае кольца. Для гэтага нада
праверыць, што выконваецца
{
}
5)
Пакажам,
что к-ца
гэта кольца з 1-й. {Трэба паказаць што
:
/ e(x)=1
}
АЗН:
(
– будзем называць кольцам палінома ад
літары х над К.
АЗН:
Пазначым
праз
СЦВ:
1)
3)
,
З
1), 2), 3) па крыт. падкольца вынікае, што
падкольца
3. Паліном як сумма аднаскладаў.
СЦВ:
Адлюстраванне
з’яўляецца
ізамарфізмам кольцаў.
1.
Праверым, што F
гомамарфізм кольцаў :
2.
{
=
}
Такім
чынам F
гомамарфізм.
З выгляду адлюстравння F адразу бачна, што яно ін’ектыўнае і сюр’ектыўнае біектыўнае F – ізамарфізм.
Вынік:
Калі
атаесаміць (отождествить) элімент
і паліном
,
то тады можна лічыць, што кольца К –
гэта падколька кольца К
.
У сэнсе такога атаесамлення мы будзем
дазваляць сабе пісаць а
замест
Абазначым:
,
x=
…
СЦВ:
Пакажам, што
ММІ
па n
n
=0:
.
Нулявая ступень у кольцы – гэта нейтральны элемент адносна множання.
Няхай выконваецца для наруральнага ліку n, тады дакажам, что яно выконваецаа для натуральнага ліку n+1.
СЦВ:
=
Вынікае
з азнач. палінома
З
гэтага моманту мы можам не рабіць разніцу
паміж
.
Замест
мы будзем гаварыць х у эннай ст. Таксама
разглядаць паліном, альбо аднасклад,
як сумму аднаскладаў.