88. Расчет резьбы на прочность

Основные виды разрушения резьб: крепежных — срез витков, ходовых — износ витков. В соответствии с этим основными критериями работоспособности и расчета для крепежных резьб являются прочность, связанная с напряжениями среза , а для ходовых резьб — износостойкость, связанная с напряжениями смятия  _см, рис. 1.17.

Условия прочности резьбы по напряжениям среза:

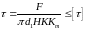для винта,

для гайки(1.12)

где H — высота гайки или глубина завинчивания винта в деталь; К = аb/р или К = се/р — коэффициент полноты резьбы; К_m — коэффициент неравномерности нагрузки по виткам резьбы.

Для треугольной резьбы К  0,87, для прямоугольной К  0,5 для трапецеидальной К  0,65; K_m  (0,6. . .0,7) —большие значения при _вв/_вг > 1,3, где _вв—предел прочности материала болта, а _вг —гайки. Это связано с тем. что увеличение относительной прочности материала винта позволяет в большей степени использовать пластические деформации в резьбе для выравнивания распределения нагрузки по виткам резьбы.

Если материалы винта и гайки одинаковы, то по напряжениям среза рассчитывают только резьбу винта, так как d₁<d.

Условие износостойкости ходовой резьбы по напряжениям смятия: 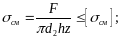(1.13)

где z = H/p — число рабочих витков (например, число витков гайки). Формула (1.13)—общая для винта и гайки. Коэффициент К_m здесь принят равным единице, с учетом приработки ходовых резьб и при условии, что допускаемые напряжения принимают согласно с накопленным опытом эксплуатации.

Высота гайки и глубина завинчивания. Равнопрочность резьбы и стержня винта является одним из условий назначения высоты стандартных гаек.

Так, например, приняв в качестве предельных напряжений пределы текучести материала на растяжение и сдвиг и учитывая, что _T = 0,6 _T,

запишем условия равнопрочности резьбы на срез и стержня винта на растяжение в виде:

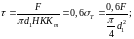
F/[(/4)d₁²] — напряжение растяжения в стержне винта, рассчитанное приближенно по внутреннему диаметру резьбы d₁. откуда при K = 0,87 и K_m  0,6 получаем:

H  0,8d₁. (1.14)

В соответствии с этим высоту нормальных стандартных гаек крепежных изделий принимают H  0,8d. (1.15)

Кроме нормальных стандартом предусмотрены высокие H  1,2 d низкие H  0,5 d гайки.

Так как d > d₁ (например, для основной крепежной резьбы d  1,2 d₁, то прочность резьбы при нормальных и высоких гайках превышает прочность стержня винта.

По тем же соображениям устанавливают глубину завинчивания винтов и шпилек в детали: в стальные детали H₁ = d, в чугунные и силуминовые H₁  1,5d.

Стандартные высоты гаек (за исключением низких) и глубины завинчивания исключают необходимость расчета на прочность резьбы стандартных крепежных деталей

Расчет на прочность стержня винта (болта) при различных случаях нагружения

С тержень винта нагружен только внешней растягивающей силой. Примером служит нарезанный участок крюка для подвешивания груза (рис. 1.18). Опасным является сечение, ослабленное нарезкой. Площадь этого сечения оценивают приближенно по внутреннему диаметру d₁ резьбы. Условие прочности по напряжениям растяжения в стержне:

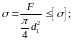
Б олт затянут, внешняя нагрузка отсутствует. Примером служат болты для крепления ненагруженных герметичных крышек и люков корпусов машин (рис. 1.19). В этом случае стержень болта растягивается осевой силой F_зат возникающей от затяжки болта, и закручивается моментом сил в резьбе Т_р—см. формулу (1.5), где F равна Fзат. Напряжение растяжения от силы F_зат, 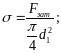Напряжение кручения от момента Т_Р : 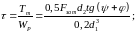Требуемое значение силы затяжки

F_зат = А _см, где А — площадь стыка деталей, приходящаяся на один болт, _см — напряжение смятия в стыке деталей, значение которого выбирают по условиям герметичности .

Прочность болта определяют по эквивалентному напряжению: (1.18)

Вычисления показывают, что для стандартных метрических резьб, _экв= 1,3 .

Это позволяет рассчитывать прочность болтов по упрощенной формуле:

(1.19) Расчетами и практикой установлено, что болты с резьбой меньше M10... .М12 можно разрушить при недостаточно квалифицированной затяжке. Например, болт с резьбой Мб разрушается при силе на ключе, равной 45Н; болт с резьбой М12 — при силе 180 H

Поэтому в среднем и тяжелом машиностроении не рекомендуют применять болты малых диаметров (меньше М8). На некоторых заводах для затяжки болтов используют специальные ключи предельного момента. Эти ключи не позволяют приложить при затяжке момент больше установленного. В таком случае отпадает необходимость ограничивать применение болтов малых диаметров (при условии, что ключи предельного момента применяют и в эксплуатации).

Болтовое соединение нагружено силами, сдвигающими детали в стыке

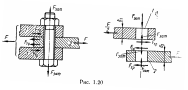Условием надежности соединения является отсутствие сдвига деталей в стыке. Конструкция может быть выполнена в двух вариантах. Болт поставлен с зазором (рис. 1.20). При этом внешнюю нагрузку F уравновешивают силами трения в стыке, которые образуются от затяжки болта. Без затяжки болтов детали могут сдвигаться на значение зазора, что не допустимо. Рассматривая равновесие детали 2, получим условие отсутствия сдвига деталей

F  iF_TP = iF_зат f, илиF_зат = K F / ( i f );

где i—число плоскостей стыка деталей (на рис. 1.20—i = 2; при соединении только двух деталей i = 1); f — коэффициент трения в стыке (f = 0,15. . .0,20 для сухих чугунных и стальных поверхностей);

К —коэффициент запаса (K =1,3...1.5 при статической нагрузке, K = 1,8. . .2 при переменной нагрузке).

Прочность болта оценивают по эквивалентному напряжению — формула (1.19).

Отметим, что в соединении, в котором болт поставлен с зазором. внешняя нагрузка не передается на болт. Поэтому болт рассчитывают только на статическую прочность по силе затяжки даже при переменной внешней нагрузке. Влияние переменной нагрузки учитывают путем выбора повышенных значений коэффициента запаса.

Б олт поставлен без зазора (рис. 1.21).

В этом случае отверстие калибруют разверткой, а диаметр стержня болта выполняют с допуском, обеспечивающим беззазорную посадку. При расчете прочности соединения не учитывают силы трения в стыке, так как затяжка болта необязательна. В общем случае болт можно заменить штифтом. Стержень болта рассчитывают по напряжениям среза и смятия.

Условие прочности по напряжениям среза:

(1.21), где i — число плоскостей среза (на рис. 1.21a, i = 2; при соединении только двух деталей — рис. 1.21, б i = 1). Закон распределения напряжений смятия по цилиндрической поверхности контакта болта и детали (рис. 1.22) трудно установить точно.

В значительной степени это зависит от точности размеров и формы деталей соединения. Поэтому расчет на смятие производят по условным напряжениям. Эпюру действительного распределения напряжений (рис. 1.22, а) заменяют условной с равномерным распределением напряжений (рис. 1.22, б).

При этом для средней детали (и при соединении только двух деталей)

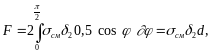
или 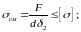для крайней детали

Формулы (1.22) справедливы для болта и деталей. Из двух значений _cм в этих формулах расчет прочности выполняют по наибольшему, а допускаемое напряжение определяют по более слабому материалу болта или детали.

Сравнивая варианты установки болтов с зазором и без зазора (см. рис. 1.20 и 1.21), следует отметить, что первый вариант дешевле второго, так как не требует точных размеров болта и отверстия. Однако условия работы болта, поставленного с зазором, хуже, чем без зазора.

Так, например, приняв коэффициент трения в стыке деталей f  0,2, K=1,5 и i = 1, из формулы (1.20) получим F_зат= 7,5F. Следовательно, расчетная нагрузка болта с зазором в 7,5 раз превышает внешнюю нагрузку. Кроме того, вследствие нестабильности коэффициента трения и трудности контроля затяжки работа таких соединений при сдвигающей нагрузке недостаточно надежна.

Болт затянут, внешняя нагрузка раскрывает стык деталей

Примером служат болты для крепления крышек резервуаров, нагруженных давлением p жидкости или газа (рис. 1.23). Затяжка болтов должна обеспечить герметичность соединения или нераскрытие стыка под нагрузкой. Задача о распределении нагрузки между элементами такого соединения статически неопределима и решается с учетом деформаций этих элементов. Обозначим: F_зат — сила затяжки болта; F=R/z — внешняя нагрузка соединения, приходящаяся на один болт (z — число болтов).

П осле приложения внешней нагрузки к затянутому соединении; болт дополнительно растянется на некоторую величину , а деформация сжатия деталей уменьшится на ту же величину.

Для простоты можно сказать, что только часть внешней нагрузки дополнительно нагружает болт, а другая часть идет на разгрузку стыка.

Если обозначим  — коэффициент внешней нагрузки (учитывает; приращение нагрузки болта в долях от силы F, то дополнительна нагрузка болта равна  F, а уменьшение затяжки стыка — (1—)F

Значение коэффициента  определяют по условию равенства дополнительных деформаций болта и деталей (условие совместности деформаций):

(1.23);

где _б — податливость болта, равная его деформации при единично нагрузке; _д — суммарная податливость соединяемых деталей.

Из равенства (1.23)

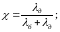(1.24)

Далее получим приращение нагрузки на болт

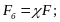(1.25)

расчетную (суммарную) нагрузку болта

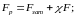(1.26)

и остаточную затяжку стыка от одного болта

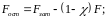(1.27)