83. Расчет нà надежность сборочных единиц

Сборочные единицы (узлы) и машин рассчитываются на на­дежность одними и теми же методами и именуются механическими системами. Механические системы могут состоять из элементов как в виде деталей машин (при расчете сборочных единиц), так и из деталей и сборочные единиц (при расчете машин). Надежность яв­ляется комплексным свойством, охватывающим безотказность, дол­говечность, ремонтопригодность и сохраняемость механических систем.

Безотказность является одной из важнейших характеристик надежности и определяется как вероятность безотказной работы механической системы в пределах заданного времени работы или требуемой наработки.

Вероятность безотказной работы механической системы может быть рассчитана различными методами, применение которых предоп­ределяется, как правило, характером исходных данных. Наиболее употребительными являются расчеты на основе вероятностей безотказной работы отдельных элементов механических систем, например деталей машин и по интенсивности отказов невосстанавливаемых систем.

Метод расчета по интенсивности отказов может быть использован и для расчета надежности восстанавливаемых систем, но до первого отказа или - после восстановления, но также до первого отказа после ремонта, т.е. при таких расчетах не учитывается время, потребное на ремонт, в то время как надежность восстанавливаемых систем рассчитывается с учетом всех потерь времени.

Интенсивностью отказов называется отношение числа отказавших образцов элементов или систем в единицу времени к среднему числу образцов, исправно работающих в данный отрезок времени при условии, что отказавшие образцы не восстанавливаются и не заменяются новыми. Эта характеристика обычно обозначается t и в ряде литературных источников называется также опасностью отказов, лямбда-характеристикой, или почасовой характеристикой

Согласно определению

где nt - число отказов образцов в интервале времени от до 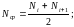- среднее число исправно работающих образцов в интервале  t; N_i, N_i+1 - соответственно число исправно работающих образцов в начале и в конце интервала  t .

Выражение (24) отображает статистическое определение ин­тенсивности отказов, а ее вероятностным определением является

где f(t) и F(t) - соответственно плотность и функция распределения случайной величины, которой в рассмат­риваемом случае является время возникновения отказа.

Зависимость между вероятностью безотказной работы и интенсивностью отказов отображаются следующим образом:

. Как следует из зависимости (25), вероятность безотказной работы может быть определена наиболее просто при постоянной интенсивности отказов, например при отображении времени отказов экспо­ненциальным распределением

Поскольку то Отказы механических систем являются, как правило, следст­вием постепенного накопления повреждений, например усталостного характера, ила ухудшения свойств из-за износа, причем отличи­тельной особенностью отказов механических систем является их проявление с "задержкой” т.е. отказы возникают по истечении некоторого времени безотказной работы. Время отказов таких сис­тем отображается трехпараметрическими распределениями, например Вейбулла и логарифмически нормального, позволяющими отображать при помощи параметра положения, т.е. "задержки", сдвиг распре­делений относительно начала координат. Для механических систем, отказы которых на начальном этапе эксплуатации маловероятны, но не исключены, характерным может оказаться бета-распределение с отрицательной асимметрией.

Ниже приводятся выражения плотности f(t) вероятности безотказной работы p(t) и интенсивности отказов (t) распределении Вейбулла 1 , логарифмически нормального 2 и бе­та-распределения 3 , на рис. 11 дано их графические изображения.

1. Распределение Вейбулла:

2. Логарифмически нормальное распределение'

3. Бета-распределение:

В этих выражениях a, b,  , (среднее значение), S (сред­нее квадратическое отклонение)  параметров распределений, t₀  параметр положения, К - параметр формы. В табл. 3 приведены [8, 9] интенсивности отказов наиболее употребительных элементов механических систем на базе 10⁵ часов, а в табл. 4 - поправочные коэффициенты К_ [9], учитывающие в виде произведения К_  отличие лабораторных условий, в которых по­лучены  , от реальных.

Следует иметь в виду, что результаты расчетов на надежность по справочным данным интенсивностей отказов могут служить лишь для ориентировочной оценки вероятности безотказной работы, поскольку ориентировочными и меняющимися в широком диапазоне являются значения самих интенсивностей отказов.

При расчете на надежность механических систем без резерви­рования структурная схема изображается в виде последовательно соединенных элементов (рис. 12), а вероятность безотказной ра­боты всей системы определяется как произведение вероятностей ее элементов