79. Расчет допускаемых напряжений для валов и осей

80. Расчет допускаемых напряжений для материалов зубчатых передач.

Р асчет на усталость при циклических контактных напряжениях, также как и при циклических нормальных или касательных напряжениях базируется на кривых усталости.

Для прямозубых передач, а также для косозубых передач с небольшой разностью твердости зубьев шестерни и колеса за расчетное принимается меньшее из двух допускаемых напряжений, определенных для материала шестерни [_H]₁ и колеса [_H]₂. При твердости больше НВ 350 за расчетное контактное напряжение принимают среднее из [_H]₁ и [_H]₂ , но не более 1,25 [_H]_min (меньшее из двух) — для цилиндрических и 1,15 [_H]_min — для конических передач.

При НВ₁ — НВ₂  70

— в числителе для цилиндрических, в знаменателе для конических передач.

_H0 — предел контактной выносливости определяется по кривым усталости. S_H = 1,1 — коэффициент безопасности ( при нормализации, улучшении или объемной закалке — однородная структура по объему), S_H = 1,2 — коэффициент безопасности при поверхностной закалке, цементации, азотировании — неоднородная структура).

K_HL — коэффициент долговечности учитывает влияние срока службы и режима нагрузки передачи:

_, где m = 6 — показатель степени кривой усталости для контактных напряжений. При K_HL  1 принимают K_HL= 1.

При переменном режиме вместо N_Hi принимают N_HE — эквивалентное число циклов по формуле:

_, при m = 6. при расчетах часто вместо отношения напряжений используют отношение моментов, то есть : напряжения пропорциональны квадратным корням из нагрузок.

При расчете допускаемых напряжений изгиба по аналогии с расчетом допускаемых контактных напряжений:

где S_F - принимают по таблицам в справочной литературе. _F - определены экспериментально для каждого материала, K_FC - коэффициент, учитывающий двухстороннее приложения нагрузки, K_FC=1 - односторонняя нагрузка; K_FC - реверсивная нагрузка, большие значения при НВ  350

K_FL — методика расчета аналогична расчету K_HL :

шлифованные зубья;

при НВ350 и нешлифованной поверхностей зубьев;

81. Расчет прочности зубьев по напряжениям изгиба.

Зуб имеет сложное напряженное состояние — см. рис. 8.10. Наибольшие напряжения изгиба образуются у корня зуба в зоне перехода эвольвенты в галтель. Здесь же наблюдаются концентрация напряжений. Для того чтобы по возможности просто получить основные расчетные зависимости и уяснить влияние основных параметров на прочность зубьев, рассмотрим вначале приближенный расчет, а затем введем поправки в виде соответствующих коэффициентов. Допустим следующее (рис.):

1. Вся нагрузка зацепления передается одной парой зубьев и приложена к вершине зуба. Практика подтверждает, что этот худший слу­чай справедлив для 7-й, 8-й и более низких степеней точности, ошибки изготовления кото­рых не могут гарантировать наличие двухпар­ного зацепления. Например (см. рис. 8.16), ошибки шага приводят к тому, что зубья начи­нают зацепляться вершинами еще до выхода на линию зацепления. При этом вместо теоретиче­ского двухпарного зацепления будет однопарное.

2. Зуб рассматриваем как консольную бал­ку, для которой справедлива гипотеза плос­ких сечений или методы сопротивления мате­риалов. Фактически зуб подобен выступу, у которого размеры поперечного сечения соизмеримы с размерами высоты. Точный расчет напряжёний в таких элементах выполняют методами теории упругости [35]. Результаты точного расчета используют для исправления приближенного расчета путем введения теоретического коэффициента концентрации напряжений (см. ниже). На расчетной схеме _, где F_t— окружная сила; _w — угол, определяющий направление нор­мальной силы F_n к оси симметрии зуба. Угол ' несколько больше угла Зацепления _w. Связь между ними — '= _w + 

1 Силу F_n переносят по линии действия на ось симметрии зуба и раскладывают на составляющие

_,

Напряжение в опасном сечении, расположенном вблизи хорды основной окружности: _, где — момент сопротивления сечения при изгибе; A=-b_ws — площадь. Знак (—) в формуле указывает, что за расчетные напряжения при­нимают напряжения на растянутой стороне зуба, так как в большин­стве случаев практики именно здесь возникают трещины усталостного разрушения (для стали растяжение опаснее сжатия).

Значения l и s неудобны для расчетов. Используя геометрическое подобие зубьев различного модуля, эти величины выражают через безразмерные коэффициенты:

где m — модуль зубьев. После подстановки и введения расчетных коэффициентов получают:

где К_F— коэффициент расчетной нагрузки; К_T — теорети­ческий коэффициент концентрации напряжений.

Далее обозначают: , коэффициент формы зуба (для наружных зубьев (см. рис. 8.20). Этот коэффициент уже рассчитан в зависимости от числа зубьев и табулирован в справочной литературе. Для колес с внутренними зубьями приближенно можно принимать Y_F = 3,5 ... 4, большее значение применьших z.

При этом для прямозубых передач расчетную формулу записывают виде:

где [_F] — допускаемое напряжение изгиба.

Для проектных расчетов по напряжениям изгиба формулу решают относительно модуля путем замены b_w =_m m;

и далее, принимая приближенно K_Fv = 1,5, получают значениями z₁ и _m задаются согласно рекомендациям.

Y_F безразмерный коэффициент, значения которого зависят только от формы зуба (размеры l', s', ) и в том числе от формы его галтели (коэффициент К_). Форма зуба, при одинаковом исходном контуре инструмента, зависит в основном от числа зубьев колеса z и коэффициента смещения инструмента х.

Рассмотрим эту зависимость.

Влияние числа зубьев на форму и прочность зубьев. На рис 8.21 показанo изменение формы зуба в зависимости от числа зубьев колес. чанных без смещения с постоянным модулем. При z   колесо превращается в рейку, и зуб приобретает прямолинейные очертания. С уменьшением z уменьшается толщина зуба у основания и вершины, а также увеличиваегся кривизна эвольвентного профиля Такое изменение формы приводит к уменьшению прочности зуба.

При дальнейшем уменьшении z появляется подрезание ножки зуба (штриховая линия на рис. 8.21), прочность зуба существенно снижается. При нарезании инструментом реечного типа для прямозубых передач число зубьев на границе подрезания Z_min= 17.

82. РАСЧЕТ ЗУБЧАТЫХ ЦИЛИНДРИЧЕСКИХ ПЕРЕДАЧ НА КОНТАКТНУЮ ВЫНОСЛИВОСТЬ.

Согласно ГОСТ 21354 — 75 формула для расчета контактных напряжений приведена в следующим виде:

Где

эту формулу используют для проверочного расчета передачи, когда все необходимые размеры и другие параметры передачи известны.

При проектном расчете необходимо определить размеры передачи по заданным основным характеристикам: крутящему моменту Т₁ или Т₂ и передаточному числу u.

С этой целью формулу решают относительно d₁ или а_. Другие неизвестные параметры оценивают приближенно или выбирают по рекомендациям на основе накопленного опыта. В нашем случае принимаем d_1  d₁; _   = 20 ; (sin 2  0,6428); K_Hv  1,15; (Этот коэффициент зависит отокружной скорости V, которая пока неизвестна, поэтому принимаем некоторое среднее значение. При этом из составляющих коэффициента K_H остается коэффициент K_H.

Обозначим _ba = b_/d₁ — коэффициент ширины шестерни относительно диаметра.

Подставляя эти значения в исходную формулу и решая ее относительно диаметра находим:

Решая относительно межосевого расстояния а_, заменяя Т₁ = Т₂/u; d₁ = 2а_ /(u+1) и вводим _ba = b_/a — коэффициент ширины колеса относительно межосевого расстояния. После преобразования, с учетом зависимости _bd = 0,5 _ba(u+1) получаем:

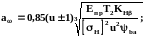
При расчете передач с цилиндрическими зубчатыми колесами чаще используют именно последнюю формулу, так как габариты передачи определяет преимущественно межосевое расстояние.

По тем же соображениям в формуле момент Т₁ заменяют на Т₂. Значения момента Т₂ — на ведомым валу является одной из основных характеристик передачи, интересующих потребителя (обычно указано в техническом задании).

В приложении к ГОСТ 21354 — 75 для стальных зубчатых колес формулы расчета записаны ввиде:

где для стальных прямозубых колес:

для косозубых колес: