52. Однокомпонентные вероятностные расчеты дм.

Однокомпонентные вероятностные расчеты применяют при подборе подшипников качения. Рассеяние долговечности подшипников качения отображается распределением Вейбулла, характеризуемого плотностью вероятности

и вероятностью безотказной работы

(8) Здесь k - параметр формы, а b - параметр масштаба распределения.

Поскольку за расчетный ресурс подшипников, приводимый в справочниках, принят гамма -процентный ресурс, равный 90%, то вероятностные расчеты подшипников ведут при вероятностях безотказной работы, больших чем p = 0,9.

Обозначив долговечности при вероятностях безотказной работы подшипников больших или равных 0,9 соответственно через Lp, L и подставив их значения в (8) вместо x , а также имея в виду, что параметр масштаба b является постоянной величиной, получим (9)Обозначим соотношение Lp/L через  учитывая, что при расчете подшипников в обычных условиях работы и вероятнос­ти безотказной работы, равной 0,9 .

полчиим формулу для определения ресурса (в млн. оборотах) .подшипников при вероятностях безотказной работы больших чем 0 ,9:

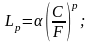где С, F, p- соответственно динамическая грузоподъемность, эквивалентная нагрузка и показатель степени в уравнении кривой усталости подшипников, а  —коэффициент, характеризующий вероятность безотказной работы.

При заданном ресурсе подобранного подшипника вероятность безотказной работы определяется по формуле, следующей из зависимости (9)

где

53. Определение расчетной нагрузки в зубчатых передачах. Коэффициенты концентрации нагрузки и динамической нагрузки и их определение.

З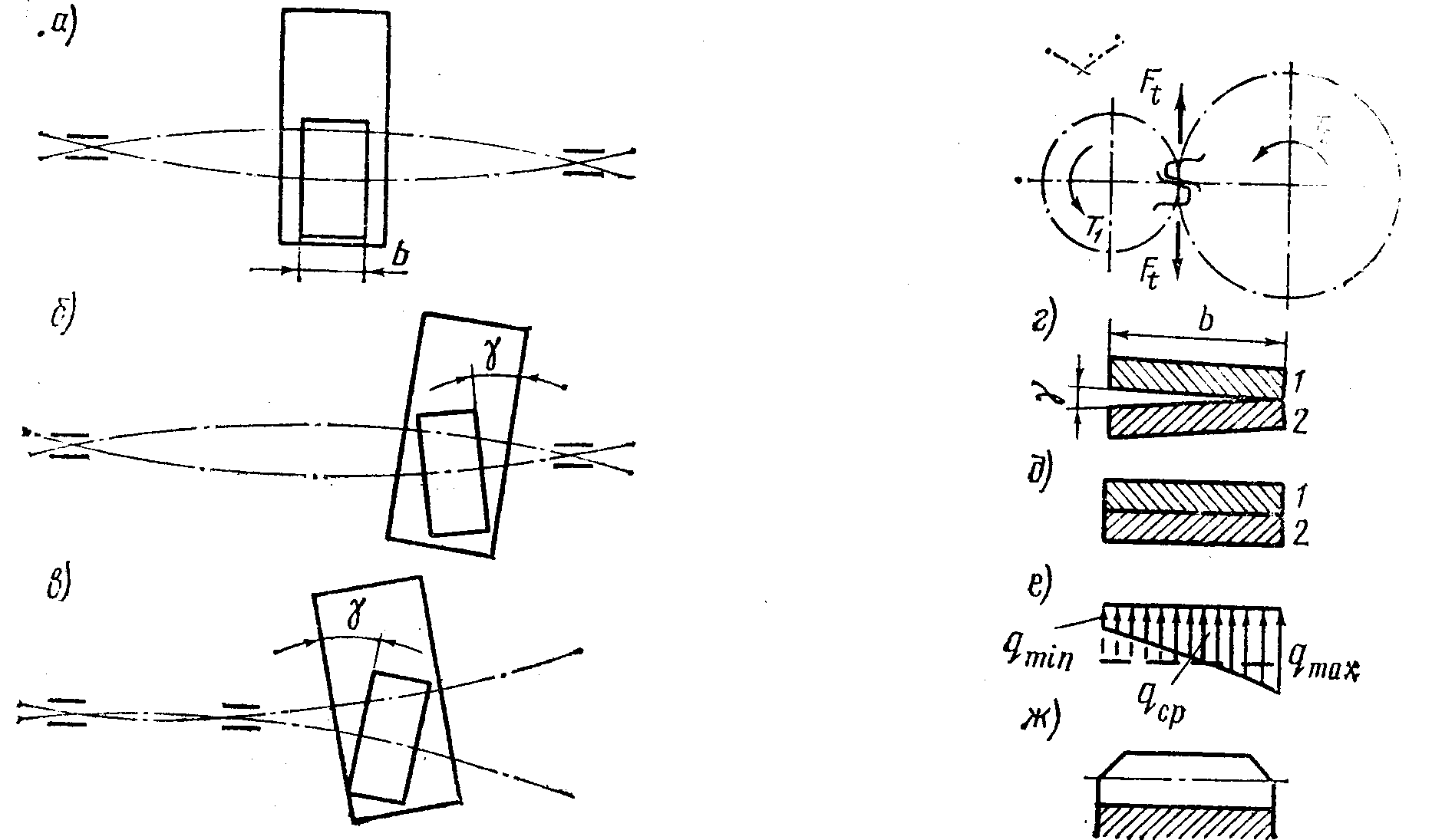 а расчетную нагрузку принимают максимальное значение удельной нагрузки, распределенной по линии контакта зубьев:

где Fn — нормальная сила в зацеплении; K=K_*K_v - коэффициент расчетной нагрузки ; K_ - коэффициент концентрации нагрузки; K_v — коэффициент динамической нагрузки; l_ — суммарная длина линии контакта зубьев.

Концентрация нагрузки и динамические нагрузки различно влияют на прочность по контактным и изгибным напряжениям. Соответственно различают K_Н; K_Н; K_Нv - при расчетах по контактным напряжениям и K_F; K_F; K_Fv - по напряжениям изгиба.

Коэффициенты концентрации нагрузки и динамической нагрузки и их определение.

Коэффициента концентрации нагрузки K. Концентрация или неравномерность распределения нагрузки по длине зуба связана с деформацией валов, опор и самих зубчатых колес, а также с погрешностями изготовления передачи. Поясним это сложное явление на примере, учитывающим только прогиб валов.

На рисунке изображено взаимное расположение зубчатых колес при деформированных валах в случаях:

1. симметричного; 2. Несимметричного; 3. консольного расположения валов.

В первом случае - перекоса нет - самый благоприятный случай.

При несимметричном и консольном расположении опор, колеса перекашиваются на угол  , что приводит к нарушению правильного касания зубьев.

При этом нагрузка перераспределяется соответственно с деформацией отдельных участков зубьев. Отношение :

где q_cp — средняя интенсивность нагрузки.

При прочих равных условиях влияние перекоса увеличивается с увеличением ширины колеса bw .

Коэффициент динамической нагрузки ,

. Выше было указано выше, что погрешности нарезания зубьев являются причиной непостоянства мгновенных значений передаточного отношения. Это значит что при ₁ = const, ₂  const.

В зацеплении появляется дополнительный динамический момент, где J — момент инерции ведомых масс. Основное влияние на значение динамических нагрузок имеют ошибки основного шага p_b. На рис. изображен случай зацепления, при котором шаг колеса больше шага шестерни, т. е. р_b2р_b1.

По закону эвольвентного зацепления i = d₂/d₁= const при постоянном положении полюса зацепления или при положении всех точек зацепления на линии зацепления А₁, А₂. Если р_b2р_b1, то вторая пара зубьев вступает в зацепление в точке b' до выхода на линию зацепления в точку b. При этом изменяется мгновенное значение передаточного отношения.

В точке b' происходит так называемый кромочный удар, который не только увеличивает динамическую нагрузку, но также способствует задиру поверхности зубьев. Для уменьшения эффекта кромочного удара применяют фланкированные зубья, у которых верхний участок эвольвенты выполняют с отклонением в тело зуба (на рис. показан штриховой линией).

Значение дополнительных динамических нагрузок зависит от значения ошибки шага, окружной скорости, присоединенных масс упругости зубьев и пр.

При p_b2 p_b1 появляется серединный удар. Для нарезания флакированных зубьев применяют тот же зуборезный инструмент, но при исходным контуре со срезами. Коэффициент К_v. определяют по формуле

где q_v — удельная динамическая нагрузка; q — удельная расчетная рабочая нагрузка в зоне ее наибольшей концентрации.

Расчет значений К_v не менее сложен, чем расчет К_ . Для прибли­женной оценки рекомендуют. Значения К_v несколько меньше при высокой твердости материала. Это объясняется не уменьшением q_v, а увеличением q вследствие увеличения допускаемых контактных напряжений.