Линейный корреляционный анализ при малом числе испытаний.
Неизбежное рассеяние результатов механических испытаний материалов и деталей машин предопределяет применение корреляционного анализа. Повышенная трудоемкость и длительность испытаний при циклических нагрузках обусловливает малое число испытаний. Отличительная особенность корреляционного анализа при малом числе (менее 30) наблюдений (испытаний) заключается в особых методах оценки доверительных границ коэффициентов корреляции, предложенных Фишером .
При ресурсных, в
частности усталостных, испытаниях
задача упрощается тем, что обычно
априорно известна (функциональная
зависимость числа циклов нагружений
от напряжении в виде
которая может быть
приведено к линейной форме логарифмированием
Результаты испытаний оформляются в воде табл. 7, итоговые данные столбцов 3...7 которой служат для последующих вычислений, а столбцов 5...7, 9 - для проверки вычислений, при этом общая сумма столбцов 5, 6 и удвоенной суши столбца 7 должна равняться сумме столбца 9. Таблица
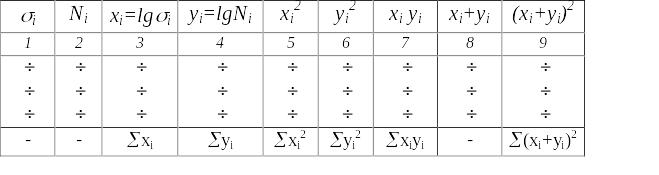
Последующие вычисления производятся по следующим формулам:
,
где n - число испытаний,
Коэффициент
корреляции
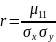
где-
смешанный центральный момент первого
порядка и Sx, Sy - средние квадратические
отклонения,
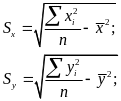
Коэффициент корреляции может принимать значения в пределах 1, при этом знак плюс соответствует положительному, а минус - отрицательному наклону прямой.
Значимость оперируемых чисел зависит от требуемой точности определения коэффициента корреляции и от ширины интервала напряжений при испытаниях ,так как при малой значимости чисел и интервала напряжений число знаков под корнем последней формулы оказывается недостаточным для вычисления Sy с необходимой точностью.Значимость коэффициента корреляции оценивается его доверительными границами, и если нижняя граница при принятом уровне значимости окажется мала, то не будет достаточных оснований (по результатам испытаний как выборки из гипотетической генеральной совокупности) считать величины x и y связанными линейной корреляцией. Считается целесообразным введение нескольких уровней значимости: линейная корреляционная связь между x и y ставится под сомнение при переходе значения коэффициента корреляции границ, соответствующих уровни значимости 0,05. В этом случае проводятся дополнительные испытания для ее проверки, безоговорочно же эта связь отбрасывается лишь при переходе границ, соответствующих уровни значимости 0,1.
При малом числе испытаний коэффициент корреляции оценивается по преобразованию, введенному Фишером
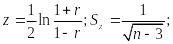в этом случае
доверительный интервал Z определяется
следующим образом
z - Sz z z + Sz;
где - коэффициент, характеризующий уровень значимости или доверительную вероятность, определяется по таблицам нормированной функции Лапласа.
По полученным граничным значениям Z определяется по таблицам функции гиперболических тангенсов доверительный интервал коэффициента корреляции и если значение его нижней границы окажется больше значения критической области, определяемой зависимостью
то это и будет
свидетельством наличия корреляционной
связи между x и y. Подстановка в
корреляционное уравнение
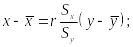значений соответствующих величин дает
уравнение прямой в логарифмических
координатах в виде
x +my = c
или с учетом принятых обозначений
потенцирование которого дает уравнение
кривой усталости в прямоугольных
координатах
где m - показатель степени уравнения
кривой усталости, C - антилогарифм числа
c
•
Прямые, проведенные слева параллельно прямой, отображающей кривую усталости в логарифмических координатах, на расстоянии 3Sx , например определяют границу значений ограниченных проделов с вероятностью не разрушения 0,9973.