1.1 Системы координат: связанная и скоростная, углы, определяющие их взаимное положение.

Рис. 1.3. Углы: тангажа – φ, рысканья - ψ и крена - γ

Положение ракеты как мат. точки в пространстве определяется прежде всего тремя координатами х, у, z в так называемой баллистической (стартовой) системе координат, связанной с Землей. За начало этой системы берут точку старта ракеты. Для баллистических ракет за ось х принимают пря­мую, перпендикулярную к ра­диусу вектору из центра Зем­ли и направленную по линии прицеливания в сторону цели (рис. 1.1). Ось у направляют по радиусу вектору вверх, а z — перпендикулярно двум пер­вым осям так, чтобы система координат была правой. Вводится еще так называемую связанную или подвижную систему осей. Начало ее нах-ся в центре масс ракеты.Ось x₁ направлена по продольной оси ракеты. Оси y_1, z₁ расположим в плоскости, перпендикулярной оси ракеты, так, чтобы на старте плоскость x₁y₁ совпадала с плоскостью ху земной системы координат, а ось z₁ имела то же направление, что и ось z. Ось y₁ называют поперечной, a z₁ - боковой осью (рис. 1.1 и 1.2). Вводят еще три угла, определяющие взаимную ориентацию осей связан­ной и стартовой систем координат. Угол между осью ракеты х₁ и плоскостью xz, т. е. угол наклона оси ракеты по отношению к стартовому горизонту, обо­значим через φ- угол тангажа (рис.1.3) Угол, который составляет ось ракеты х₁ с плоскостью ху, обо­значим через ψ - угол рыскания. Он характери­зует отклонение оси ракеты от плоскости х,у. Угол, определяющий поворот корпуса ракеты относительно ее продольной оси – угол крена γ между осью y₁ и пло­скостью ху.

1.2 Идеальная скорость одноступенчатой ракеты – формула Циолковского.

Идеальная скорость V_k представляет собой верхний предел достижимой скорости в идеальных условиях.

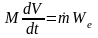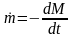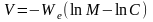Из ур-ия движения ракеты и выражения реактивной силы Можно определить скорость, которую может получить ракета в идеальном случае, когда ее движение происходит не только за пре­делами атмосферы, но и вне поля тяготения Земли. учитывая получим Так как эффективная скорость истечения W_e остается величиной постоянной, после интегрирования получим где С — произвольная постоянная.

При V = 0 масса ракеты равна начальной массе М₀ (суммар­ной массе конструкции, полезного груза и топлива). Поэтому

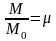
По мере выгорания топлива масса М и соответственно вели­чина µ уменьшаются, а скорость V возрастает. Когда двигатель будет выключен, скорость достигнет своего наибольшего конеч­ного значения

2.1 Силы, действующие на ракету в полете, их задание в системах координат.

Основными силами, оп­ределяющими движение центра масс ракеты, являются: сила тяги, собственный вес ра­кеты, аэродинамические силы и силы на управляющих органах. Как и всякое тело, движущееся в воздухе, газе или жидко­сти, ракета испытывает со стороны среды действие сил трения и давления на поверхности. Значения этих сил и законы их распределения зависят от многих факторов и в первую очередь от скорости полета. Статическая составляющая сил атмосфер­ного давления уже была нами учтена при выводе выраже­ния тяги Поэтому при определении аэродинамических сил необходимо рассматривать лишь увеличение давления по срав­нению со статическим у головной части и его понижение у донного среза. Это избыточное (положительное или отрицательное) давление вместе с силами аэродинамического трения дает рав­нодействующую, которая называется полной аэродинамической силой.

При анализе законов движения ракеты и вообще летатель­ного аппарата полную аэродинамическую силу раскладывают обычно по скоростным осям x₂, у₂ и z₂ на составляющие X, Y, Z.