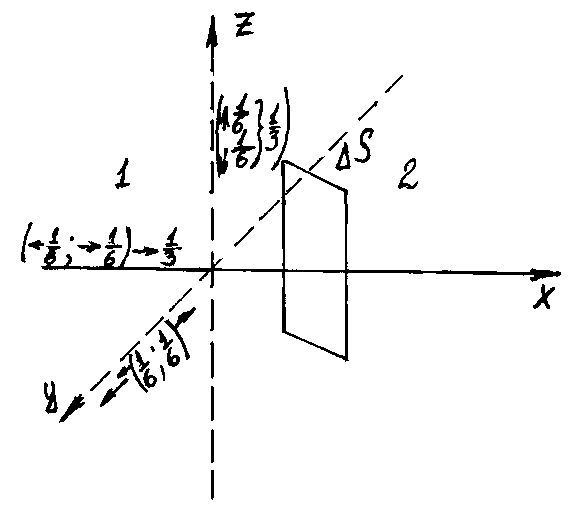- •33.Явление переноса.
- •35.Политропный процесс
- •Принцип суперпозиции электрических полей
- •41.Работа электростатического поля по перемещению заряда
- •Плоскость
- •44.Свободные и связанные заряды. Потенциал электрического поля при наличии диэлектриков. Зависимость поляризации от поля
- •Электродвижущая сила
- •Напряжение
- •Единицы электродвижущей силы
26.Волны - это изменение состояния среды (возмущения), распространяющиеся в этой среде и несущие с собой энергию и импульс без переноса вещества. Наиболее часто встречающиеся виды волн — упругие (звук) и электромагнитные (свет, радиоволны и другие).
Примером волнового движения может быть возмущение воды от падающих капель, которое распространяется в виде расширяющихся концентрических кругов.
Волновое уравнение: A = A0 cos(ωt + kx)
.
Уравнение плоской бегущей волны.
Гармоническая бегущая волна является плоской волной, т.к. ее волновые поверхности
(ω(t-)+φ0)=const представляет собой совокупности плоскостей, параллельных друг другу и перпендикулярных оси х.
S(0)=A0cos(ωt+φ0)
1).S(x)=A0cos(ω(t-r)+φ0)=A0cos(ω(t-)+φ0)-распространение волны вдоль положительного направления оси х.
(ω(t-)+φ0)=const
dt==0,=-фазовая скорость.
2). S(x)=A0cos(ω(t+r)+φ0)=A0cos(ω(t-)+φ0)
к=- волновое число
S(x)=A0cos(ω(t-r)+φ0)=A0cos(ω(t-)+φ0)= A0cos(ωt-)+φ0)=A0cos(ωt- kх+φ0)
Если имеется среда, то: S(х)=A0cos(ωt-kх+φ0), А-амплитуда плоскости х=0,
S(х)=A0cos(ωt-+φ0), - скалярное произведение волнового вектора и радиус-вектора .
.
Энергия упругой волны
Найдем полную механическую энергию (5.8.2) для выделенного нами элемента упругой среды, в которой распространяются упругая продольная волна:
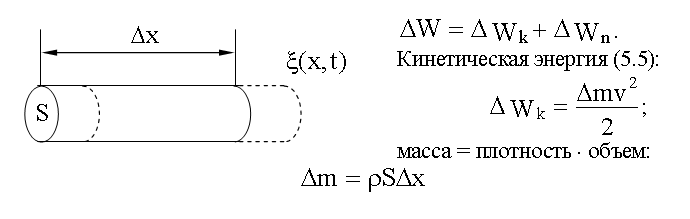 .
.
Скорость (3.8.2):
![]() ,
тогда
,
тогда
![]()
.
Потенциальная энергия упругого деформированного стержня:
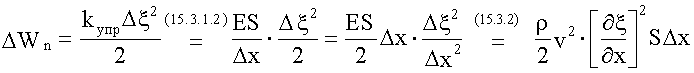 .
.
Полная энергия выделенного элемента объемом SΔx будет равна:
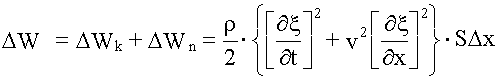 .
.
Плотность энергии упругой волны
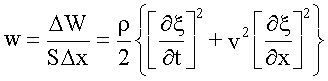 .
.
Пло́тность пото́ка эне́ргии — физическая величина, численно равная потоку энергии через единичную площадку, перпендикулярную направлению потока. Часто вводят также вектор плотности потока энергии (так называемый вектор Умова), величина которого равна плотности потока энергии, а направление совпадает с направлением потока. В электродинамике вектор плотности потока электромагнитной энергии носит название вектора Пойнтинга.
Плотность потока энергии
![]()
27.Интерференция волн — взаимное увеличение или уменьшение результирующей амплитуды двух или нескольких когерентных волн, одновременно распространяющихся в пространстве.[1] Сопровождается чередованием максимумов и минимумов (пучностей) интенсивности в пространстве. Результат интерференции (интерференционная картина) зависит от разности фаз накладывающихся волн.
Необходимые условия для наблюдения интерференции:
1) волны должны иметь одинаковые (или близкие) частоты, чтобы картина, получающаяся в результате наложения волн, не менялась во времени (или менялась не очень быстро, что бы её можно было успеть зарегистрировать);
2) волны должны быть однонаправленными (или иметь близкое направление); две перпендикулярные волны никогда не дадут интерференции (попробуйте сложить две перпендикулярные синусоиды!). Иными словами, складываемые волны должны иметь одинаковые волновые векторы (или близконаправленные).
Волны, для которых выполняются эти два условия, называются КОГЕРЕНТНЫМИ. Первое условие иногда называют временной когерентностью, второе - пространственной когерентностью.
Рассмотрим в качестве примера результат сложения двух одинаковых однонаправленных синусоид. Варьировать будем только их относительный сдвиг. Иными словами, мы складываем две когерентные волны, которые отличаются только начальными фазами (либо их источники сдвинуты друг относительно друга, либо то и другое вместе).
Если синусоиды расположены так, что их максимумы (и минимумы) совпадают в пространстве, произойдет их взаимное усиление.
Если же синусоиды сдвинуты друг относительно друга на полпериода, максимумы одной придутся на минимумы другой; синусоиды уничтожат друг друга, то есть произойдет их взаимное ослабление.
Математически это выглядит так. Складываем две волны:
![]()
![]()
здесь х1 и х2 - расстояния от источников волн до точки пространства, в которой мы наблюдаем результат наложения. Квадрат амплитуды результирующей волны (пропорциональный интенсивности волны) дается выражением:
![]()
Максимум этого выражения есть 4A2, минимум - 0; всё зависит от разности начальных фаз и от так называемой разности хода волн D:
![]()
При
![]() в
данной точке пространства будет
наблюдаться интерференционный максимум,
при
в
данной точке пространства будет
наблюдаться интерференционный максимум,
при
![]() -
интерференционный минимум.
-
интерференционный минимум.
Стоя́чая волна́ — колебания в распределённых колебательных системах с характерным расположением чередующихся максимумов (пучностей) и минимумов (узлов) амплитуды. Практически такая волна возникает при отражениях от преград и неоднородностей в результате наложения отражённой волны на падающую. При этом крайне важное значение имеет частота, фаза и коэффициент затухания волны в месте отражения.
Примерами стоячей волны могут служить колебания струны, колебания воздуха в органной трубе[1]; в природе — волны Шумана.
Чисто стоячая волна, строго говоря, может существовать только при отсутствии потерь в среде[2] и полном отражении волн от границы. Обычно, кроме стоячих волн, в среде присутствуют и бегущие волны, подводящие энергию к местам её поглощения или излучения.
Для демонстрации стоячих волн в газе используют трубу Рубенса.
В случае гармонических колебаний в одномерной среде стоячая волна описывается формулой:
![]() ,
,
где
u
— возмущения в точке х
в момент времени t,
![]() —
амплитуда
стоячей волны,
—
амплитуда
стоячей волны,
![]() —
частота , k
— волновой
вектор,
—
частота , k
— волновой
вектор,
![]() —
фаза.
—
фаза.
Стоячие волны являются решениями волновых уравнений. Их можно представить себе как суперпозицию волн, распространяющихся в противоположных направлениях.
При существовании в среде стоячей волны, существуют точки, амплитуда колебаний в которых равна нулю. Эти точки называются узлами стоячей волны. Точки, в которых колебания имеют максимальную амплитуду, называются пучностями.
Математическое описание стоячих волн
В одномерном случае две волны одинаковой частоты, длины волны и амплитуды, распространяющиеся в противоположных направлениях (например, навстречу друг другу), будут взаимодействовать, в результате чего может возникнуть стоячая волна. Например, гармоничная волна, распространяясь вправо, достигая конца струны, производит стоячую волну. Волна, что отражается от конца, должна иметь такую же амплитуду и частоту, как и падающая волна.
Рассмотрим падающую и отраженную волны в виде:
![]()
![]()
где:
y0 — амплитуда волны,
— циклическая (угловая) частота, измеряемая в радианах в секунду,
k — волновой вектор, измеряется в радианах на метр, и рассчитывается как
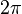 поделённое
на длину волны
поделённое
на длину волны
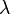 ,
,x и t — переменные для обозначения длины и времени.
Поэтому результирующее уравнение для стоячей волны y будет в виде суммы y1 и y2:
![]()
Используя тригонометрические соотношения, это уравнение можно переписать в виде:
![]()
Если
рассматривать моды
![]() и
антимоды
и
антимоды
![]() ,
то расстояние между соседними модами
/ антимодами будет равно половине длины
волны
,
то расстояние между соседними модами
/ антимодами будет равно половине длины
волны
![]() .
.
Волновое уравнение
Для того, чтобы получить стоячие волны как результат решения однородного дифференциального волнового уравнения (Даламбера)
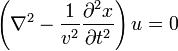
необходимо соответствующим образом задать его граничные условия (например, закрепить концы струны).
В общем случае неоднородного дифференциального уравнения
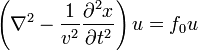 ,
,
где
![]() выполняет
роль «силы», с помощью которой
осуществляется смещение в определенной
точке струны, стоячая волна возникает
автоматически
выполняет
роль «силы», с помощью которой
осуществляется смещение в определенной
точке струны, стоячая волна возникает
автоматически
28.Термодинамическая система — это некая физическая система, состоящая из большого количества частиц, способная обмениваться с окружающей средой энергией и веществом. Также обычно полагается, что такая система подчиняется статистическим закономерностям. Для термодинамических систем справедливы законы термодинамики.
Для описания термодинамической системы вводят так называемые термодинамические величины — набор физических величин, значения которых определяют термодинамическое состояние системы. Примерами термодинамических величин являются:
температура
давление
объём
внутренняя энергия
энтропия
энтальпия
свободная энергия Гельмгольца
энергия Гиббса
Если термодинамическое состояние системы не меняется со временем, то говорят, что система находится в состоянии равновесия. Строго говоря, термодинамические величины, приведённые выше, могут быть определены только в состоянии термодинамического равновесия.
Внутреннюю энергию тела нельзя измерить напрямую. Можно определить только изменение внутренней энергии:
![]()
где
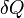 —
подведённое
к телу количество теплоты, измеренное
в джоулях
—
подведённое
к телу количество теплоты, измеренное
в джоулях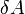 [1]
— работа,
совершаемая телом против внешних сил,
измеренная в джоулях
[1]
— работа,
совершаемая телом против внешних сил,
измеренная в джоулях
Эта формула является математическим выражением первого начала термодинамики
Для квазистатических процессов выполняется следующее соотношение:
![]()
где
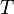 —
температура,
измеренная в кельвинах
—
температура,
измеренная в кельвинах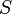 —
энтропия,
измеренная в джоулях/кельвин
—
энтропия,
измеренная в джоулях/кельвин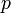 —
давление,
измеренное в паскалях
—
давление,
измеренное в паскалях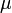 —
химический
потенциал
—
химический
потенциал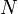 —
количество
частиц в системе
—
количество
частиц в системе
Понятие энтропии впервые было введено Клаузиусом в термодинамике в 1865 году для определения меры необратимого рассеивания энергии, меры отклонения реального процесса от идеального. Определённая как сумма приведённых теплот, она является функцией состояния и остаётся постоянной при обратимых процессах, тогда как в необратимых — её изменение всегда положительно.
![]() ,
,
где
![]() —
приращение энтропии;
—
приращение энтропии;
![]() —
минимальная теплота, подведенная к
системе; T — абсолютная температура
процесса;
—
минимальная теплота, подведенная к
системе; T — абсолютная температура
процесса;
Свобо́дная эне́ргия Гельмго́льца (или просто свобо́дная эне́ргия) — термодинамический потенциал, убыль которого в квазистатическом изотермическом процессе равна работе, совершённой системой над внешними телами.
Свободная энергия Гельмгольца для системы с постоянным числом частиц определяется так:
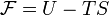 ,
где
,
где
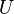 —
внутренняя
энергия,
—
внутренняя
энергия,
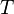 —
абсолютная температура,
—
абсолютная температура,
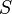 —
энтропия.
—
энтропия.
Свободная энергия Гиббса (или просто энергия Гиббса, или потенциал Гиббса, или термодинамический потенциал в узком смысле) — это величина, показывающая изменение энергии в ходе химической реакции и дающая таким образом ответ на вопрос о принципиальной возможности протекания химической реакции; это термодинамический потенциал следующего вида:
![]()
где
—
внутренняя
энергия,
![]() —
давление,
—
давление,
![]() —
объём,
—
абсолютная температура,
—
энтропия.
—
объём,
—
абсолютная температура,
—
энтропия.
Основные положения МКТ
Молекулярно-кинетической теорией называют учение о строении и свойствах вещества на основе представления о существовании атомов и молекул как наименьших частиц химических веществ.
В основе молекулярно-кинетической теории лежат три основных положения:
Все вещества – жидкие, твердые и газообразные – образованы из мельчайших частиц – молекул, которые сами состоят из атомов («элементарных молекул»). Молекулы химического вещества могут быть простыми и сложными, т.е. состоять из одного или нескольких атомов. Молекулы и атомы представляют собой электрически нейтральные частицы. При определенных условиях молекулы и атомы могут приобретать дополнительный электрический заряд и превращаться в положительные или отрицательные ионы.
Атомы и молекулы находятся в непрерывном хаотическом движении.
Частицы взаимодействуют друг с другом силами, имеющими электрическую природу. Гравитационное взаимодействие между частицами пренебрежимо мало.
29.
Закон о равномерном распределении энергии по степеням свободы |
Итак, средняя энергия приходящаяся на одну степень свободы:
У одноатомной молекулы i = 3, тогда для одноатомных молекул
для двухатомных молекул
для трёхатомных молекул
Таким образом, на среднюю кинетическую энергию молекулы, имеющей i-степеней свободы, приходится
Это и есть закон Больцмана о равномерном распределении средней кинетической энергии по степеням свободы. Если
система находится в состоянии
термодинамического равновесия, при
температуре Т,
то средняя кинетическая энергия
равномерно распределена между всеми
степенями свободы. На каждую
поступательную iп
и вращательную iвр
степени свободы приходится энергия
1/2
kT.
Для колебательной iкол,
степени свободы она равна kT.
Таким образом число степеней свободы
i
= iп
+ iвр
+ 2iкол
Закон
о равномерном распределении энергии
по степеням свободы перестает быть
справедливым при квантовом описании
системы частиц, когда каждому квантовому
состоянию системы с i-степенями
свободы соответствует ячейка объемом
hi
в фазовом пространстве “координаты
– импульсы” тождественных (неразличимых
между собой) частиц, где h
– постоянная Планка (М. Планк (1858-1947)
– немецкий физик–теоретик).
При
этом энергии вращения и колебания
молекул принимают дискретные значения
или говорят, что они квантуются. Энергия
колебания молекулы (как квантового
гармонического осциллятора равна
Eкол
= (1/2+n)
hv,
где v
– собственная частота колебаний; n
= 0,1,2,… - квантовое число.
Энергия
Eкол
при n
= 0, равная E0
= 1/2 hv,
называется нулевой колебательной
энергией (энергией
нулевых колебаний).
Разность энергий ΔEкол
между соседними уровнями энергии
равна hv.
Энергия вращательного движения
молекулы зависит от её вида. Для
двухатомной молекулы с жесткой связью
эта энергия имеет видЕвр
=
Для
одноатомных газов это выполняется в
очень широких пределах, а для двухатомных
газов только в интервале от 100 до 1000
К. Отличие связано с проявлением
квантовых законов. При низких
температурах вращательное движение
как бы «вымерзает» и двухатомные
молекулы движутся поступательно, как
одноатомные; равны их теплоёмкости.
При увеличении температуры, когда
Т
> 1000 К, начинают сказываться колебания
атомов молекулы вдоль оси z
(атомы в молекуле связаны не жёстко,
а как бы на пружине). Одна колебательная
степень свободы несет
|
30.Уравнение состояния идеального газа (иногда уравнение Клапейрона или уравнение Менделеева — Клапейрона) — формула, устанавливающая зависимость между давлением, молярным объёмом и абсолютной температурой идеального газа. Уравнение имеет вид:
![]()
где
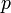 —
давление,
—
давление,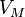 —
молярный
объём,
—
молярный
объём,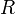 —
универсальная
газовая постоянная
—
универсальная
газовая постоянная— абсолютная температура,К.
Так
как
![]() ,
где
,
где
![]() —
количество
вещества,
а
—
количество
вещества,
а
![]() ,
где
,
где
![]() —
масса,
—
масса,
![]() —
молярная
масса,
уравнение состояния можно записать:
—
молярная
масса,
уравнение состояния можно записать:
![]()
Эта форма записи носит имя уравнения (закона) Менделеева — Клапейрона.
В случае постоянной массы газа уравнение можно записать в виде:
![]()
![]()
Последнее уравнение называют объединённым газовым законом. Из него получаются законы Бойля — Мариотта, Шарля и Гей-Люссака:
![]() —
закон
Бойля — Мариотта.
—
закон
Бойля — Мариотта.
![]() —
Закон
Гей-Люссака.
—
Закон
Гей-Люссака.
![]() —
закон
Шарля
(второй закон Гей-Люссака, 1808
г.)
—
закон
Шарля
(второй закон Гей-Люссака, 1808
г.)
А
в форме пропорции
![]() этот
закон удобен для расчёта перевода газа
из одного состояния в другое.
этот
закон удобен для расчёта перевода газа
из одного состояния в другое.
С точки зрения химика этот закон может звучать несколько иначе: Объёмы вступающих в реакцию газов при одинаковых условиях (температуре, давлении) относятся друг к другу и к объёмам образующихся газообразных соединений как простые целые числа. Например, 1 объём водорода соединяется с 1 объёмом хлора, при этом образуются 2 объёма хлороводорода:
![]()
1 объём азота соединяется с 3 объёмами водорода с образованием 2 объёмов аммиака:
![]()
— закон Бойля — Мариотта.
Закон Бойля — Мариотта назван в честь ирландского физика, химика и философа Роберта Бойля (1627—1691), открывшего его в 1662 г., а также в честь французского физика Эдма Мариотта (1620—1684), который открыл этот закон независимо от Бойля в 1677 году.
В некоторых случаях (в газовой динамике) уравнение состояния идеального газа удобно записывать в форме
![]()
где
![]() —
показатель
адиабаты,
—
показатель
адиабаты,
![]() —
внутренняя энергия единицы массы
вещества.
—
внутренняя энергия единицы массы
вещества.
Эмиль Амага обнаружил, что при высоких давлениях поведение газов отклоняется от закона Бойля — Мариотта. И это обстоятельство может быть прояснено на основании молекулярных представлений.
С одной стороны, в сильно сжатых газах размеры самих молекул являются сравнимыми с расстояниями между молекулами. Таким образом, свободное пространство, в котором движутся молекулы, меньше, чем полный объём газа. Это обстоятельство увеличивает число ударов молекул в стенку, так как благодаря ему сокращается расстояние, которое должна пролететь молекула, чтобы достигнуть стенки.
С
другой стороны, в сильно сжатом и,
следовательно, более плотном газе
молекулы заметно притягиваются к другим
молекулам гораздо большую часть времени,
чем молекулы в разреженном газе. Это,
наоборот, уменьшает число ударов молекул
в стенку, так как при наличии притяжения
к другим молекулам молекулы газа движутся
по направлению к стенке с меньшей
скоростью, чем при отсутствии притяжения.
При не слишком больших давлениях более
существенным является второе обстоятельство
и произведение
![]() немного
уменьшается. При очень высоких давлениях
большую роль играет первое обстоятельство
и произведение
увеличивается.
немного
уменьшается. При очень высоких давлениях
большую роль играет первое обстоятельство
и произведение
увеличивается.
31.Закон распределения молекул идеального газа по скоростям, теоретически полученный Максвеллом в 1860 г. определяет, какое число dN молекул однородного (p = const) одноатомного идеального газа из общего числа N его молекул в единице объёма имеет при данной температуре Т скорости, заключенные в интервале от v до v + dv.
Для вывода функции распределения молекул по скоростям f(v) равной отношению числа молекул dN, скорости которых лежат в интервале v ÷ v + dv к общему числу молекул N и величине интервала dv
![]()
Максвелл использовал два предложения:
а) все направления в пространстве равноправны и поэтому любое направление движения частицы, т.е. любое направление скорости одинаково вероятно. Это свойство иногда называют свойством изотропности функции распределения.
б)
движение по трем взаимно перпендикулярным
осям независимы т.е. х-компоненты скорости
![]() не
зависит от того каково значения ее
компонент
не
зависит от того каково значения ее
компонент
![]() или
или![]() .
И тогда вывод f
(v)
делается сначала для одной компоненты
,
а затем обобщается на все координаты
скорости.
.
И тогда вывод f
(v)
делается сначала для одной компоненты
,
а затем обобщается на все координаты
скорости.
Считается также, что газ состоит из очень большого числа N тождественных молекул находящихся в состоянии беспорядочного теплового движения при одинаковой температуре. Силовые поля на газ не действуют.
Функции f (v) определяет относительное число молекул dN(v)/N скорости которых лежат в интервале от v до v + dv (например: газ имеет N = 106 молекул, при этом dN = 100
молекул
имеют скорости от v
=100 до v
+ dv
=101 м/с (dv
=
1 м![]() )
тогда
)
тогда
![]() .
.
Используя методы теории вероятностей, Максвелл нашел функцию f (v) - закон распределения молекул идеального газа по скоростям:
![]()
f (v ) зависит от рода газа (от массы молекулы) и от параметра состояния (от температуры Т)
f(v)
зависит от отношения кинетической
энергии молекулы, отвечающей рассматриваемой
скорости
![]() к
величине kT
характеризующей среднюю тепловую
энергию молекул газа.
к
величине kT
характеризующей среднюю тепловую
энергию молекул газа.
П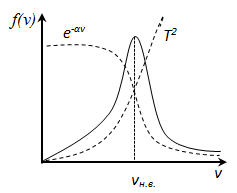 ри
малых v
ри
малых v
![]() и
функция f(v)
изменяется практически по параболе
и
функция f(v)
изменяется практически по параболе
![]() .
При возрастании v множитель
.
При возрастании v множитель
![]() уменьшается
быстрее, чем растет множитель
уменьшается
быстрее, чем растет множитель![]() ,
т.е. имеется max функции f(v).
Скорость, при которой функция распределения
молекул идеального газа по скоростям
максимальна, называется наиболее
вероятной скоростью
,
т.е. имеется max функции f(v).
Скорость, при которой функция распределения
молекул идеального газа по скоростям
максимальна, называется наиболее
вероятной скоростью![]() найдем из условия
найдем из условия
![]()
![]()
![]()
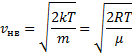
![]() ,
следовательно, с ростом температуры
наиболее вероятная скорость растёт, но
площадь S,
ограниченная кривой функции распределения
остаётся неизменной, так как из условия
нормировки
,
следовательно, с ростом температуры
наиболее вероятная скорость растёт, но
площадь S,
ограниченная кривой функции распределения
остаётся неизменной, так как из условия
нормировки
![]() (так
как вероятность достоверного события
равна 1), поэтому при повышении температуры
кривая распределения f
(v)
будет растягиваться и понижаться.
(так
как вероятность достоверного события
равна 1), поэтому при повышении температуры
кривая распределения f
(v)
будет растягиваться и понижаться.
В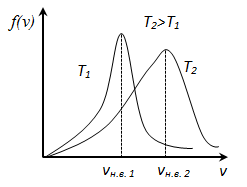 статистической физике среднее значение
какой-либо величины определяется как
интеграл от 0 до бесконечности произведения
величины на плотность вероятности этой
величины (статистический вес)
статистической физике среднее значение
какой-либо величины определяется как
интеграл от 0 до бесконечности произведения
величины на плотность вероятности этой
величины (статистический вес)
<X>=![]()
Тогда средняя арифметическая скорость молекул
![]()
и интегрируя по частям получили
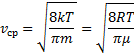
Скорости, характеризующие состояние газа
Барометрическая формула — зависимость давления или плотности газа от высоты в поле тяжести.
Для
идеального
газа,
имеющего постоянную температуру
и
находящегося в однородном поле тяжести
(во всех точках его объёма ускорение
свободного падения
![]() одинаково),
барометрическая формула имеет следующий
вид:
одинаково),
барометрическая формула имеет следующий
вид:
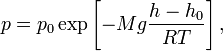
где
![]() —
давление газа в слое, расположенном на
высоте
—
давление газа в слое, расположенном на
высоте
![]() ,
,
![]() —
давление на нулевом уровне (
—
давление на нулевом уровне (![]() ),
),
![]() —
молярная
масса
газа,
—
молярная
масса
газа,
![]() —
газовая
постоянная,
—
абсолютная
температура.
Из барометрической формулы следует,
что концентрация молекул
—
газовая
постоянная,
—
абсолютная
температура.
Из барометрической формулы следует,
что концентрация молекул
![]() (или
плотность газа) убывает с высотой по
тому же закону:
(или
плотность газа) убывает с высотой по
тому же закону:
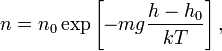
где
![]() —
масса молекулы газа,
—
масса молекулы газа,
![]() —
постоянная
Больцмана.
—
постоянная
Больцмана.
Барометрическая формула может быть получена из закона распределения молекул идеального газа по скоростям и координатам в потенциальном силовом поле (см. Статистика Максвелла — Больцмана). При этом должны выполняться два условия: постоянство температуры газа и однородность силового поля. Аналогичные условия могут выполняться и для мельчайших твёрдых частичек, взвешенных в жидкости или газе. Основываясь на этом, французский физик Ж. Перрен в 1908 году применил барометрическую формулу к распределению по высоте частичек эмульсии, что позволило ему непосредственно определить значение постоянной Больцмана.
Барометрическая
формула показывает, что плотность газа
уменьшается с высотой по экспоненциальному
закону. Величина
![]() ,
определяющая быстроту спада плотности,
представляет собой отношение потенциальной
энергии частиц к их средней кинетической
энергии, пропорциональной
,
определяющая быстроту спада плотности,
представляет собой отношение потенциальной
энергии частиц к их средней кинетической
энергии, пропорциональной
![]() .
Чем выше температура
,
тем медленнее убывает плотность с
высотой. С другой стороны, возрастание
силы тяжести
.
Чем выше температура
,
тем медленнее убывает плотность с
высотой. С другой стороны, возрастание
силы тяжести
![]() (при
неизменной температуре) приводит к
значительно большему уплотнению нижних
слоев и увеличению перепада (градиента)
плотности. Действующая на частицы сила
тяжести
может
изменяться за счёт двух величин: ускорения
и
массы частиц
.
(при
неизменной температуре) приводит к
значительно большему уплотнению нижних
слоев и увеличению перепада (градиента)
плотности. Действующая на частицы сила
тяжести
может
изменяться за счёт двух величин: ускорения
и
массы частиц
.
Следовательно, в смеси газов, находящейся в поле тяжести, молекулы различной массы по-разному распределяются по высоте.
Реальное распределение давления и плотности воздуха в земной атмосфере не следует барометрической формуле, так как в пределах атмосферы температура и ускорение свободного падения меняются с высотой и географической широтой. Кроме того, атмосферное давление увеличивается с концентрацией в атмосфере паров воды.
Барометрическая
формула лежит в основе барометрического
нивелирования
— метода определения разности высот
![]() между
двумя точками по измеряемому в этих
точках давлению (
между
двумя точками по измеряемому в этих
точках давлению (![]() и
и
![]() ).
Поскольку атмосферное давление зависит
от погоды, интервал времени между
измерениями должен быть возможно
меньшим, а пункты измерения располагаться
не слишком далеко друг от друга.
Барометрическая формула записывается
в этом случае в виде:
).
Поскольку атмосферное давление зависит
от погоды, интервал времени между
измерениями должен быть возможно
меньшим, а пункты измерения располагаться
не слишком далеко друг от друга.
Барометрическая формула записывается
в этом случае в виде:
![]() (в
м), где
(в
м), где
![]() —
средняя температура слоя воздуха между
точками измерения,
—
средняя температура слоя воздуха между
точками измерения,
![]() —
температурный коэффициент объёмного
расширения воздуха. Погрешность при
расчётах по этой формуле не превышает
0,1—0,5 % от измеряемой высоты. Более точна
формула Лапласа, учитывающая влияние
влажности воздуха и изменение ускорения
свободного падения.
—
температурный коэффициент объёмного
расширения воздуха. Погрешность при
расчётах по этой формуле не превышает
0,1—0,5 % от измеряемой высоты. Более точна
формула Лапласа, учитывающая влияние
влажности воздуха и изменение ускорения
свободного падения.
32.
Число столкновений и средняя длина свободного пробега молекул в газах |
Обозначим
Медленность явлений переноса, например диффузии ароматических веществ – «распространение запаха», - при относительно высокой скорости теплового движения молекул (103 м/с) объясняется столкновениями молекул. Молекула газа время от времени сталкивается с другими молекулами. В момент столкновения молекула резко изменяет величину и направление скорости своего движения. Расстояние, проходимое молекулой в среднем без столкновений, называется средней длиной свободного пробега. Средняя длина свободного пробега равна:
где
Модель идеального газа – твёрдые шарики одного диаметра, взаимодействующие между собой только при столкновении.Обозначим σ – эффективное сечение молекулы, т.е. полное поперечное сечение рассеяния, характеризующее столкновение между двумя молекулами (рис. 3.2).
За одну секунду молекула проходит путь, равный средней арифметической скорости . За ту же секунду молекула претерпевает ν столкновений. Следовательно,
Подсчитаем число столкновений ν. Вероятность столкновения трех и более молекул бесконечно мала. Предположим, что все молекулы застыли, кроме одной. Её траектория будет представлять собой ломаную линию. Столкновения будут только с теми молекулами, центры которых лежат внутри цилиндра радиусом d (рис. 3.3).
Путь,
который пройдет молекула за одну
секунду, равен длине цилиндра
На самом деле, все молекулы движутся (и в сторону, и навстречу друг другу), поэтому число соударений определяется средней скоростью движения молекул относительно друг друга. По закону сложения случайных величин
А
так как средняя длина свободного
пробега
Уравнение состояния идеального газа позволяет нам выразить n через давление P и термодинамическую температуру Т. Так
как
Таким образом, при заданной температуре средняя длина свободного пробега обратно пропорциональна давлению Р:
Например,
при d
= 3 Å = 3×10-10 м, Р
= 1 атм., Т
= 300 К, |
33.Явление переноса.
До сих пор рассматривался газ, находящийся в равновесном состоянии, т.е. когда во всех точках занимаемого объема такие величины, как T, P и n – концентрация молекул одинаковые.
Рассмотрим процессы, возникающие при отклонении газа от равновесия.
Явления (процессы), возникающие в газах при отклонении их от равновесия, называются явлениями переноса.
К этим явлениям относятся диффузия, теплопроводность и внутреннее трение. Все явления переноса связаны с выравниванием того или иного физического параметра в результате хаотического теплового движения молекул.
Процесс установления внутри фаз равновесного распределения концентрации газовых молекул (а также молекул жидких и твёрдых тел) называется диффузией.
Процесс направленного переноса внутренней энергии (выравнивание температуры) называется теплопроводностью.
Процесс направленного переноса количества движения (связано с возникновением сил трения между слоями) называется внутренним трением.
В газах все эти явления связаны с нарушением максвелловского распределения молекул по скоростям. Во всех этих явлениях мы имеем дело с переносом в газе какой-либо физической величины:
тепла ΔQ – теплопроводность;
количества движения ΔL – внутреннее трение;
массы ΔM – диффузия.
|
Основа вывода всех уравнений едина, а именно: выбирается покоящаяся среда и выравнивание той или иной величины происходит исключительно благодаря неупорядоченному тепловому движению молекул (нет перемешивания). Т.к. движение газовых молекул беспорядочно, то любое из возможных движений считается равновероятным. Выбирается произвольная площадка ΔS и рассматривается переход молекул из одной области в другую через площадку за время Δt. Обозначая переносимую величину за B, получим:
|
где k – коэффициент пропорциональности;
– коэффициент теплопроводности;
Д – коэффициент диффузии;
– коэффициент вязкости;
![]() –
градиент
вдоль направления Х:
–
градиент
вдоль направления Х:
dH = dT – температуры;
dH = dn – концентрации;
dH = dv – скорости;
dB – переносимая величина:
dB = dQ – теплота;
dB = dM – масса;
dB = dF – сила (количество движения).
Тогда получаем систему уравнений:
![]() –
уравнение
теплопроводности;
–
уравнение
теплопроводности;
![]() –
уравнение
диффузии (1-й закон Фика);
–
уравнение
диффузии (1-й закон Фика);
![]() –
уравнение
внутреннего трения
–
уравнение
внутреннего трения
З![]() нак
“–“ указывает, что процесс происходит
в сторону убывания градиента.
нак
“–“ указывает, что процесс происходит
в сторону убывания градиента.
Коэффициенты имеют значения:
![]() , (20)
, (20)
где Cудv – удельная теплоёмкость при V = const;
– плотность;
![]() –
средняя длина свободного пробега;
–
средняя длина свободного пробега;
![]() –
средняя
скорость движения молекулы.
–
средняя
скорость движения молекулы.
Сопоставляя формулы уравнения (20), видно, что один коэффициент может быть получен из другого.
Связь между коэффициентами:
= η·Судv = Д·Судv·ρ (21)
Пример:
характеристики газовых молекул при нормальных условиях:
Газ |
|
× 104 м |
|
O2 |
187 |
6,47 |
57 |
CO2 |
139 |
3,97 |
33 |
H2O (при 1000С) |
90 |
4,04 |
50 |
Уравнения переноса, рассмотренные для газов, имеют более общий характер, т.е. они частично годны для жидких и твёрдых тел.
34.Первый закон термодинамики является обобщением закона сохранения и превращения энергии для термодинамической системы. Он формулируется следующим образом:
Изменение ΔU внутренней энергии неизолированной термодинамической системы равно разности между количеством теплоты Q, переданной системе, и работой A, совершенной системой над внешними телами.
|
Соотношение, выражающее первый закон термодинамики, часто записывают в другой форме:
|
Количество теплоты, полученное системой, идет на изменение ее внутренней энергии и совершение работы над внешними телами.
Первый закон термодинамики является обобщением опытных фактов. Согласно этому закону, энергия не может быть создана или уничтожена; она передается от одной системы к другой и превращается из одной формы в другую. Важным следствием первого закона термодинамики является утверждение о невозможности создания машины, способной совершать полезную работу без потребления энергии извне и без каких-либо изменений внутри самой машины. Такая гипотетическая машина получила название вечного двигателя (perpetuum mobile) первого рода. Многочисленные попытки создать такую машину неизменно заканчивались провалом. Любая машина может совершать положительную работу A над внешними телами только за счет получения некоторого количества теплоты Q от окружающих тел или уменьшения ΔU своей внутренней энергии.
Применим первый закон термодинамики к изопроцессам в газах.
В изохорном процессе (V = const) газ работы не совершает, A = 0. Следовательно,
Q = ΔU = U (T2) – U (T1).
Здесь U (T1) и U (T2) – внутренние энергии газа в начальном и конечном состояниях. Внутренняя энергия идеального газа зависит только от температуры (закон Джоуля). При изохорном нагревании тепло поглощается газом (Q > 0), и его внутренняя энергия увеличивается. При охлаждении тепло отдается внешним телам (Q < 0).
В изобарном процессе (p = const) работа, совершаемая газом, выражается соотношением
A = p (V2 – V1) = p ΔV.
Первый закон термодинамики для изобарного процесса дает:
Q = U (T2) – U (T1) + p (V2 – V1) = ΔU + p ΔV.
При изобарном расширении Q > 0 – тепло поглощается газом, и газ совершает положительную работу. При изобарном сжатии Q < 0 – тепло отдается внешним телам. В этом случае A < 0. Температура газа при изобарном сжатии уменьшается, T2 < T1; внутренняя энергия убывает, ΔU < 0.
В изотермическом процессе температура газа не изменяется, следовательно, не изменяется и внутренняя энергия газа, ΔU = 0.
Первый закон термодинамики для изотермического процесса выражается соотношением
|
Количество теплоты Q, полученной газом в процессе изотермического расширения, превращается в работу над внешними телами. При изотермическом сжатии работа внешних сил, произведенная над газом, превращается в тепло, которое передается окружающим телам.
Наряду с изохорным, изобарным и изотермическим процессами в термодинамике часто рассматриваются процессы, протекающие в отсутствие теплообмена с окружающими телами. Сосуды с теплонепроницаемыми стенками называются адиабатическими оболочками, а процессы расширения или сжатия газа в таких сосудах называются адиабатическими.

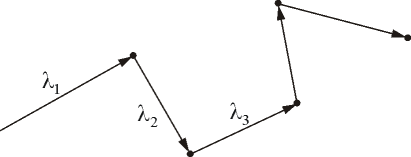 Рис.
3.1
Рис.
3.1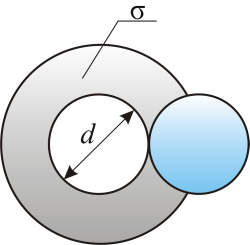 Рис.
3.2
Рис.
3.2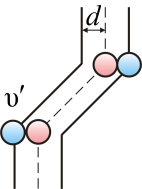 Рис.
3.2
Рис.
3.2