26.Волновое движение.

Волна - это возмущение, распространяющееся с конечной скоростью в пространстве и несущее с собой энергию. Суть волнового движения состоит в переносе энергии без переноса вещества.

Любое возмущение связано с каким-то направлением (вектор электрического поля в электромагнитной волне, направление колебаний частиц при звуковых волнах, градиент концентрации, градиент потенциала и т.д.). По взаимоположению вектора возмущения и вектора скорости волны, волны подразделяются на продольные (направление вектора возмущения совпадает с направлением вектора скорости) и поперечные (вектор возмущения перпендикулярен вектору скорости).

Уравнение плоской незатухающей бегущей волны.

S=So Sin(Wot-kt) – уравнение плоской бегущей волны

Уравнение плоской волны, распространяющейся вдоль положительного направления оси х

                             

(S(x, t) — смещение точек среды с координатой х в момент времени /; А — амплитуда волны; ω— циклическая (круговая) частота; k — волновое число; λ—длина волны; v — фазовая скорость; Т— период колебаний; φ0 — начальная фаза колебаний).

Упру́гие во́лны (звуковые волны) — волны, распространяющиеся в жидких, твёрдых и газообразных средах за счёт действия упругих сил.

Энергия упругой волны.

Найдем полную механическую энергию (5.8.2) для выделенного нами элемента упругой среды, в которой распространяются упругая продольная волна:

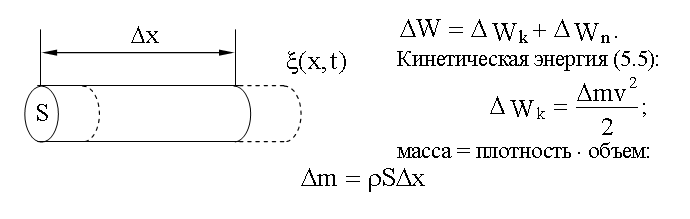Скорость (3.8.2):

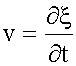
тогда

.

Потенциальная энергия упругого деформированного стержня:

.

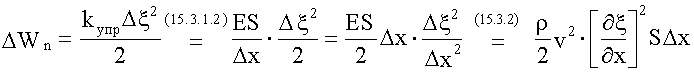Полная энергия выделенного элемента объемом SΔx будет равна:

.

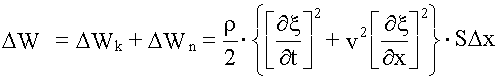Плотность энергии упругой волны

.

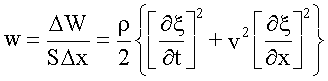Бегущими называются волны которые переносят в пространстве энергию.

Вектор плотности потока энергии (вектор Умова)

Характеризуется переносом энергии в волнах , совпадает по направлению с направлением скорости распространения волн и равен произведению обьемной плотности энергии на вектор скорости распространения волны .

Вектор Умова  можно определить через векторное произведение двух векторов:

 (в системе СИ),

где E и H — векторы напряжённости электрического и магнитного полей соответствен

27. Сложение (Интерференция) волн — взаимное увеличение или уменьшение результирующей амплитуды двух или нескольких когерентных волн, одновременно распространяющихся в пространстве.^[1] Сопровождается чередованием максимумов и минимумов (пучностей) интенсивности в пространстве. Результат интерференции (интерференционная кар

Стоя́чая волна́ — колебания в распределённых колебательных системах с характерным расположением чередующихся максимумов (пучностей) и минимумов (узлов) амплитуды. Практически такая волна возникает приотражениях от преград и неоднородностей в результате наложения отражённой волны на падающую. При этом крайне важное значение имеет частота, фаза и коэффициент затухания волны в месте отражения.

Примерами стоячей волны могут служить колебания струны, колебания воздуха в органной трубе^[1]; в природе —волны Шумана.

Чисто стоячая волна, строго говоря, может существовать только при отсутствии потерь в среде^[2] и полном отражении волн от границы. Обычно, кроме стоячих волн, в среде присутствуют и бегущие волны, подводящие энергию к местам её поглощения или излучения.

Для демонстрации стоячих волн в газе используют трубу Рубенса.

тина) зависит от разности фаз накладывающихся волн

28. Термодинамическая система — это любая область пространства, ограниченная действительными или воображаемыми границами, выбранными для анализа её внутренних термодинамических параметров.

Пространство, смежное с границей системы, называется внешней средой. У всех термодинамических систем есть среда, с которой может происходить обмен энергии и вещества.

Границы термодинамической системы могут быть неподвижными или подвижными.

Системы могут быть большими или маленькими, в зависимости от границ.

Система может существовать в вакууме или может содержать несколько фаз одного или более веществ. Термодинамические системы могут содержать сухой воздух и водяной пар (два вещества) или воду и водяной пар (две стадии одного и того же вещества). Однородная система состоит из одного вещества, одной его фазы или однородной смеси нескольких компонентов.

Системы бывают изолированными (замкнутыми) или открытыми. В изолированной системе не происходит никаких обменных процессов с внешней средой. В открытой системе и энергия и вещество могут переходить из системы в среду и обратно.

Состояние термодинамической системы определяется физическими свойствами вещества. Температура, давление, объем, внутренняя энергия, энтальпия и энтропия — это термодинамические величины, определяющие те или иные интегральные параметры системы. Данные параметры строго определяются лишь для систем, находящихся в состоянии термодинамического равновесия.

Различают экстенсивные параметры состояния, пропорциональные массе термодинамической системы, и интенсивные параметры состояния, не зависящие от массы системы. К экстенсивным параметрам состояния. относятся: объём, Внутренняя энергия, Энтропия, Энтальпия, изохорно-изотермический потенциал Гиббсова энергия), изобарно-изометрический потенциал (Гельмгольцева энергия); к интенсивным параметрам состояния— давление, температура, концентрация, магнитная индукция и др. параметры состояния взаимосвязаны, так что равновесное состояние системы можно однозначно определить, установив значения ограниченного числа параметров состояния.

В молекулярно-кинетической теории поль зуются идеализированной моделью идеаль ного газа, согласно которой:

1) собственный объем молекул газа пренебрежимо мал по сравнению с объемом сосуда;

2) между молекулами газа отсутству ют силы взаимодействия;

3) столкновения молекул газа между собой и со стенками сосуда абсолютно упругие.

Модель идеального газа можно ис пользовать при изучении реальных газов, так как они в условиях, близких к нормальным (например, кислород и гелий), а также при низких давлениях и высоких температурах близки по своим свойствам к идеальному газу.