
- •21.Средние величины, их сущность, виды, функции.
- •22. Средняя арифметическая простая и взвешенная, понятие и порядок расчёта.
- •23. Средняя гармоническая, геометрическая и квадратическая: понятие и порядок расчёта.
- •24.Мода и медиана как структурные средние. Другие структурные средние.
- •25.Понятие и показатели вариации.
- •26.Понятие о выборочном обследовании, этапы его проведения.
- •27.Показатели выборочного наблюдения.
- •28.Понятие и виды связи в статистике.
- •29.Ряд динамики: сущность, виды, элементы и особенности.
- •30.Средние показатели в рядах динамики.
- •31.Методы сопоставимости рядов динамики.
- •32.Определение тенденции развития рядов динамики.
- •33.Основные методы обработки и анализа рядов динамики.
- •34.Приведение рядов динамики к единому основанию.
- •35.Статистические индексы: понятие, виды и роль в изучении социально-экономических явлений.
- •36.Индивидуальные и общие индексы.
- •37.Агрегатные индексы. Порядок построения индексов качественных показателей.
- •38.Агрегатные индексы. Порядок построения индексов объёмных показателей.
- •39. Средние индексы: сущность и порядок расчёта.
25.Понятие и показатели вариации.
Вариация — колеблемость, многообразие, изменяемость величины признака у единиц совокупности.
Вариация, порождаемая существенными факторами, носит систематический характер, т.е. наблюдается последовательное изменение вариантов признака в определенном направлении. Такая вариация называется систематической. Вариация, обусловленная случайными факторами, называется случайной вариацией. Все изменения носят хаотический характер, поскольку нет устойчивой связи этих факторов с единицами изучаемой совокупности.
Вариация зависимого признака, образовавшаяся под действием всех без исключения влияющих на него факторов, называется общей вариацией. Следовательно, общая вариация слагается из систематической и случайной вариации.
Показатели вариации делятся на две группы: абсолютные и относительные.
Абсолютные показатели
1. Размах колебаний, или размах вариации — разница между максимальным и минимальным значениями признака в изучаемой совокупности:
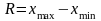
2.
Среднее
линейное отклонение
—
среднее арифметическое значение
абсолютных отклонений признака от его
среднего уровня:
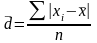 —
простая средняя
—
простая средняя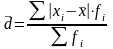 —взвешенная
средняя
—взвешенная
средняя
3. Дисперсия признака, определяемая на основе квадратической степенной средней (представляет собой средний квадрат отклонений индивидуальных значений признака от их средней величины):
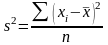 —простая
дисперсия
—простая
дисперсия —
взвешенная дисперсия
—
взвешенная дисперсия
4. Среднее квадратическое отклонение — представляет собой корень квадратный из дисперсии; обобщающая характеристика размеров вариации признака в совокупности (показывает, на сколько в среднем отклоняются конкретные варианты признака от среднего значения):
 —простая
средняя
—простая
средняя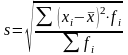 —
взвешенная средняя
—
взвешенная средняя
Относительные показатели - эти показатели вычисляются как отношение абсолютных показателей вариации к средней арифметической (или медиане):
— коэффициент
осциляции:
отражает относит меру колеблемости
крайних значений признака вокруг
средней

— относительное
линейное отклонение:
отражает долю усредненного значения
абсол отклонений от средней величины
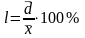
— коэффициент
вариации:
используется для оценки типичности
средних величин и позволяет представить
дисперсию как долю от средней величины
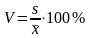 .
.
— квартиль:
рассчитывается на основе соотношения
между верхней и нижней квартилей и
медианой
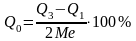
Относительные показатели вариации применяются для сравнения колеблимости различных признаков одной совок-сти, одного и того же признака в неск совок-стях; для установления однородности совок-сти.
Коэффициент вариации применяется наиболее часто. Его используют для сравнительной оценки вариации, для характеристики однородности совокупности (совокупность считается однородной, если коэффициент вариации не превышает 33 %), для сравнительной оценки колеблемости одного признака в различных совокупностях.
