19.2.Расчет пружин
19.2.1Силы в пружине
Расчет пружин
растяжения и сжатия одинаков. Пружины
сжатия, у которых отношение высоты к
диаметру
,
являются длинными. Такие пружины
необходимо вставлять в гильзу или
надевать на оправку, чтобы избежать
перекоса.
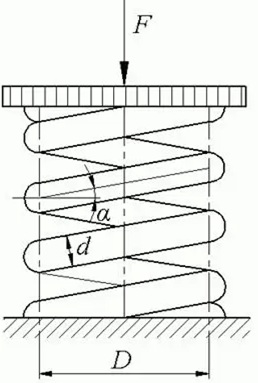
Рис. 19.7 – Основные параметры пружины: F – сила сжатия (растяжения); D – диаметр пружины; d – диаметр проволоки; α – угол наклона витков
Угол наклона
,
иначе расчет даст неверные результаты.
В поперечном
сечении витка возникают два внутренних
силовых фактора: поперечная сила
и крутящий момент
.
Угол наклона из-за его малости не
учитывается.
Рис. 19.8 – Силы в поперечном сечении витка пружины
В поперечном сечении витка возникают только касательные напряжения. При этом:
Касательные напряжения, связанные с наличием крутящего момента,
определяются так же, как при кручении прямого бруса круглого поперечного сечения.
Касательные напряжения, связанные с наличием поперечной силы,
распределены по сечению равномерно.
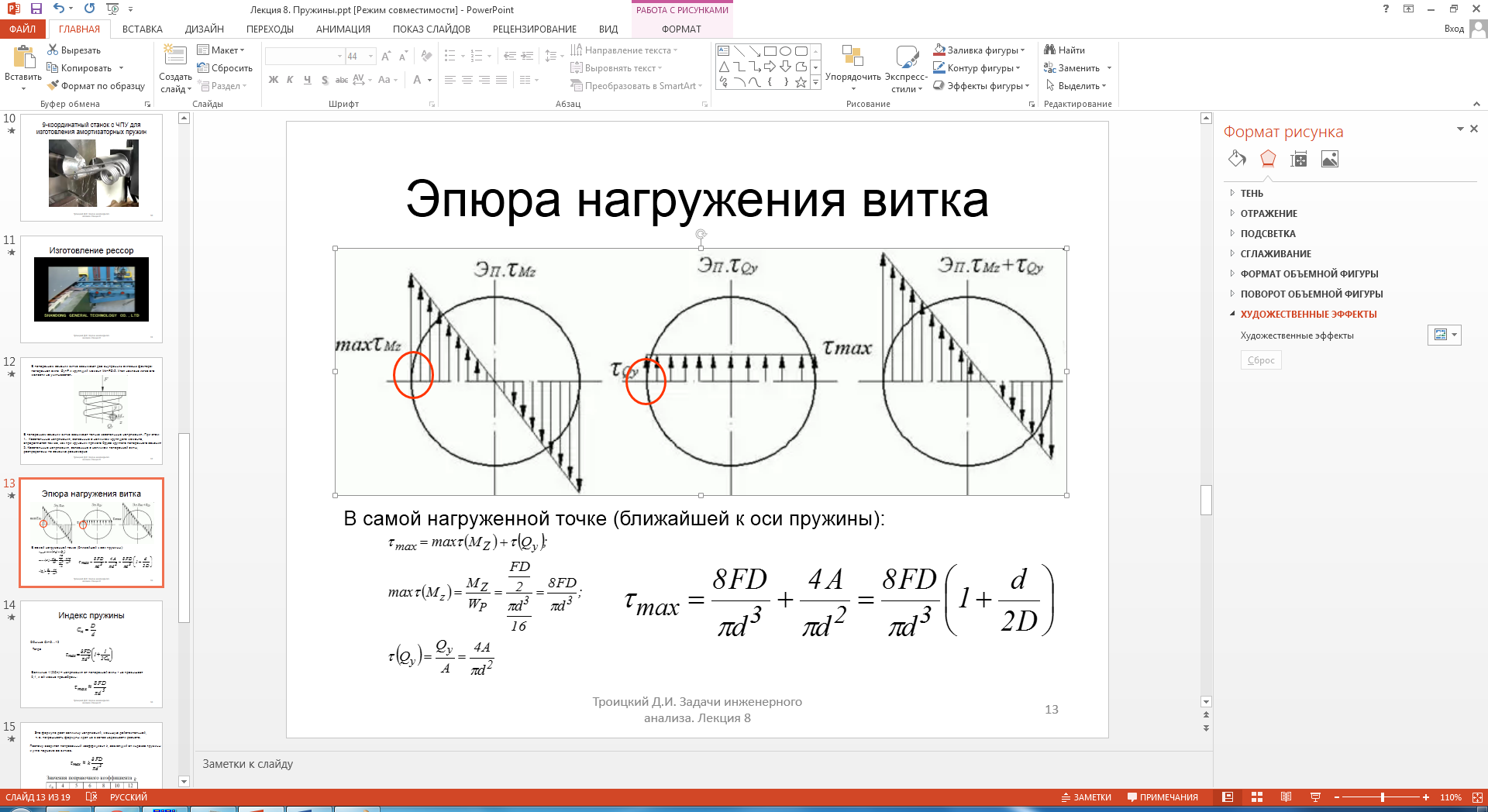
Рис. 19.9 – Эпюра нагружения витка
В самой нагруженной точке (ближайшей к оси пружины):
19.2.2Индекс пружины
Индекс пружины рассчитывается по формуле:
Обычно индекс
принимается равным
Тогда:
Величина
– напряжения от поперечной силы – не
превышает 0,1 и ей можно пренебречь:
Эта формула дает величину напряжений, меньшую действительной, т. е. погрешность формулы идет не в запас надежности расчета. Поэтому вводится поправочный коэффициент k, зависящий от индекса пружины и угла подъема ее витков:
Таблица 17.1. Значения поправочного коэффициента
|
4 |
5 |
6 |
8 |
10 |
12 |
|
1,37 |
1,29 |
1,24 |
1,17 |
1,14 |
1,11 |
Примерная формула для вычисления поправочного коэффициента:
19.2.3Расчет размера пружины под нагрузкой (осадки пружины)
Работа внешней статически приложенной силы определяется по теореме Клапейрона:
где – сила, приложенная к пружине, – максимальное перемещение точки приложения силы (осадки пружины).
Формулировка теоремы Клапейрона: упругая работа внешней силы при статическом приложении равна половине произведения ее окончательного значения на соответствующее этой силе перемещение.
Энергия деформации пружины:
где 
– полная длина проволоки пружины,
(
– число витков);
– модуль сдвига;
–
геометрическая характеристика сечения.
Тогда:
Итоговая формула для вычисления осадки пружины:
20.Список литературы
1. Тьюарсон Р. Разреженные матрицы / Пер. с англ. М.: Мир, 1977. 191 с.
2. Брамеллер А., Аллан Р., Хэмэм Я. Слабозаполненные матрицы / Пер. с англ. М.: Энергия, 1979. 192 с.
3. Эстербю О., Златев 3. Прямые методы для разреженных матриц / Пер. с англ. М.: Мир, 1987. 120 с.
4. Писсанецки С. Технология разреженных матриц / Пер. с англ. М.: Мир, 1988. 410 с.
5. Сабоннадьер Ж.-К., Кулон Ж.-Л. Метод конечных элементов и САПР / Пер. с англ. М.: Мир, 1989. 192 с.
6. Станкевич И. В. Численные методы линейной алгебры: Учеб. пособие. М.: МГТУ им. Н. Э. Баумана, 1991. 44 с.
7. Самарский А. А., Николаев Е. С. Методы решения сеточных уравнений. М.: Наука, 1978. 592 с.
8. Хойгеман Л., Янг Д. Прикладные итерационные методы / Пер. с англ. М.: Мир, 1986. 448 с.