18.3.Момент затяжки

Крутящий момент на ключе идет на преодоление момента, создаваемого силой трения торца гайки о неподвижную опорную поверхность стягиваемых деталей и момента сопротивления в резьбе:

, (18.1)

где M_R - момент, необходимый для создания осевого усилия и преодоления трения в резьбе, Н·м; M_T - момент сил трения на торцевой поверхности гайки, головки винта или его упорного конца, Н·м.

, (18.2)

где F_ZAT – усилие затяжки, Н; f_T – коэффициент трения по торцу; R_TR – приведенный радиус трения, для кольца:

(18.3)

Момент сопротивления в резьбе:

, (18.4)

где d₂ - средний диаметр резьбы, м.

(18.5)

(18.6)

, (18.7)

где d– диаметр отверстия под болт; P – шаг резьбы; β – угол подъема винтовой линии резьбы; f_R – коэффициент трения в резьбе.

Окончательная формула:

(18.8)

По ней определяется момент затяжки в зависимости от силы F_ZAT, которую должно удерживать резьбовое соединение.

18.4.Расчет соединений в WinMachine

В WinMachine существует модуль APM Joint, предназначенный для расчета прочности соединений. При запуске модуля выбираем болтовое соединение с зазором (рис. 18.9).

Рис. 18.6 – Выбор типа соединения в модуле APM Joint

Для расчета группы винтов, нагруженных произвольной нагрузкой, следует задать геометрию поверхности, находящейся в контакте. Ее можно создать с помощью инструментов модуля АРМ Joint, либо импортировать форму поверхности стыка из других графических систем посредством формата DXF. Окончательным этапом создания поверхности стыка является указание внешнего и внутреннего контуров( ) (Рис 18.10).

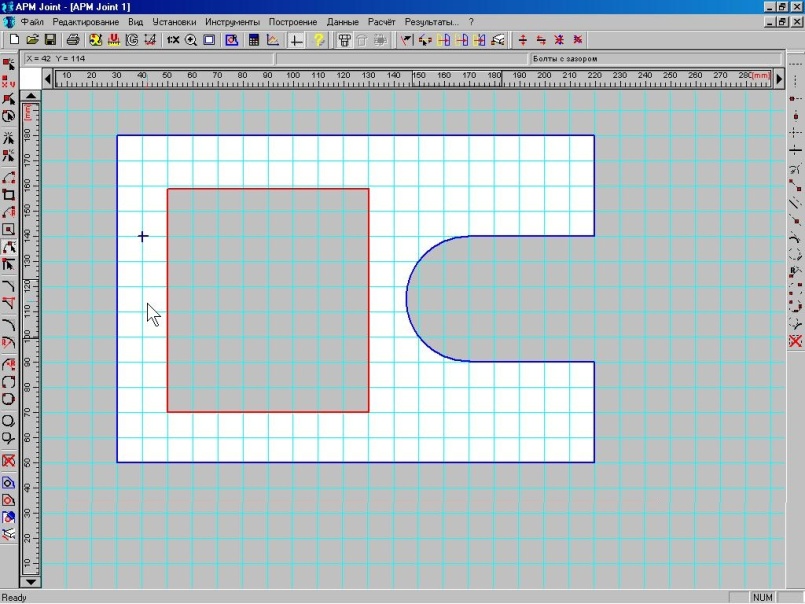
Рис. 18.10 – Пример созданной поверхности

После создания поверхности стыка нужно указать местоположение болтов ( ) и задать приложенные к соединению нагрузки ( ). Завершающий этап перед проведением расчета - выбор материала крепежных элементов и задание постоянных параметров (коэффициентов запаса)( ). В результате расчета по критерию статической прочности определяются размеры крепежных элементов, а также карта нагрузок на винты и карта удельных давлений на поверхность контакта. По карте нагрузок можно судить об эффективности использования каждого из винтов, а по карте давлений на поверхность (рис. 18.11) - о прочности этой поверхности.

Рис. 18.11 – Карта давлений на поверхность

В случае неудовлетворительной усталостной прочности можно вручную изменить диаметр винтов, либо поменять материал, из которого они изготовлены.

19.Пружины

19.1.Основные понятия

Пружина – упругий элемент, предназначенный для накапливания и поглощения механической энергии

По виду воспринимаемой нагрузки среди пружин выделяют:

• пружины сжатия;

• пружины растяжения;

• пружины кручения;

• пружины изгиба.

Пружины растяжения – рассчитаны на увеличение длины под нагрузкой (рис. 19.1). В ненагруженном состоянии обычно имеют сомкнувшиеся витки. На концах для закрепления пружины на конструкции имеются крючки или кольца.

Рис. 19.1 – Пружина растяжения

Пружины, работающие на растяжение, подвергаются продольно-осевой нагрузке, т. е. под действием нагрузки растягиваются вдоль оси пружины. При снятии нагрузки пружина принимает исходное положение – сжимается.

Пружины сжатия – рассчитаны на уменьшение длины под нагрузкой. Витки таких пружин без нагрузки не касаются друг друга (рис. 19.2). Концевые витки поджимают к соседним и торцы пружины шлифуют. Длинные пружины сжатия, во избежание потери устойчивости, ставят на оправки или стаканы. Пружины, работающие на сжатие, подвергаются продольно-осевой нагрузке и сжимаются под ее действием. При снятии этой нагрузки пружина принимает исходное положение – расправляется.

Рис. 19.2 – Пружина сжатия

Витки пружин растяжения-сжатия под действием постоянной по величине силы испытывают напряжения двух видов: изгиба и кручения.

Пружины кручения — могут быть двух видов:

• торсионные — стержень, работающий на кручение (рис. 19.3);

• витые пружины, работающие на кручение (как в бельевых прищепках, в мышеловках и в канцелярских дыроколах).

Рис. 19.3 – Пружина кручения (торсион)

Пружины, работающие на кручение, подвергаются нагрузке моментом от пары сил, действующих в параллельных плоскостях, перпендикулярных оси на нагрузку одновременно. Для устранения закручивания торцовых опор и перекоса пружины размещают одну в другой с последовательным сочетанием правой и левой навивки пружины. В основном пружины кручения работают на изгиб. Такие пружины широко применяют в технике, как пружины прижимные, возвратные и как упругие звенья силовых передач.

Плоские пружины работают только на изгиб под действием изгибающих нагрузок (рис. 19.4). К плоским пружиним относят рессоры, широко применяемые в железнодорожном и автомобильном транспорте.

Рис. 19.4 – Плоская пружина изгиба

Ярким примером применения пружин является подвеска автомобиля (рис. 19.5).

Рис. 19.5 – Применение пружин в подвеске автомобиля: а – подвеска McPherson; б – торсионная подвеска; в – классическая пружинная подвеска

Характеристика пружины показывает зависимость деформации пружины от нагрузки на нее (рис. 19.6). Характеристика может быть линейной (жесткость остается постоянной при любой деформации) или прогрессивной (жесткость увеличивается).

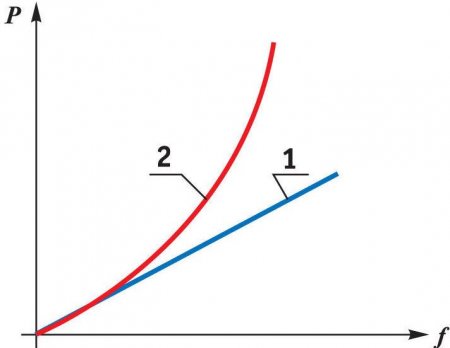
Рис. 19.6 – Зависимость деформации пружины f от ее нагрузки P: 1 – линейная, 2 – нелинейная