16.Зубчатые передачи

Зубчатой передачей называется меха­низм, служащий для передачи вращательного движения с одного вала на другой и изменения частоты вращения посредством зубчатых колес и реек.

Зубчатое колесо, сидящее на передающем вращение валу, называется веду­щим, а на получающем вращение — ведомым. Меньшее из двух колес со­пряженной пары называют шестерней; большее — колесом; тер­мин «зубчатое колесо» относится к обеим деталям передачи.

Зубчатые передачи представляют собой наиболее распространенный вид передач в современном машиностроении. Они очень надежны в работе, обеспечивают постоянство передаточного числа, компактны, имеют высо­кий КПД, просты в эксплуатации, долговечны и могут передавать любую мощность (до 36 тыс. кВт).

К недостаткам зубчатых передач следует отнести: необходимость высо­кой точности изготовления и монтажа, шум при работе со значительными скоростями, невозможность бесступенчатого изменения передаточного числа.

В связи с разнообразием условий эксплуатации формы элементов зубча­тых зацеплений и конструкции передач весьма разнообразны.

16.1.Эвольвентное зацепление

Боковые грани зубьев, соприкасаю­щиеся друг с другом во время враще­ния колес, имеют специальную кри­волинейную форму, называемую про­филем зуба. Наиболее распространен­ным в машиностроении является эвольвентный профиль(рис. 16.1).

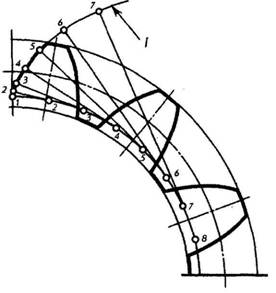
Рис. 16.1 – Эвольвентный профиль зубчатого колеса.

Придание профилям зубьев зубча­тых зацеплений таких очертаний не является случайностью. Чтобы зубья двух колес, находящихся в зацепле­нии, могли плавно перекатываться один по другому, необходимо было вы­брать такой профиль для зубьев, при котором не происходило бы перекосов и защемления головки одного зуба во впадине другого.

На рис. 16.2 изображена пара зубчатых колес, находящихся в зацепле­нии. Линия, соединяющая центры колес О₁ и О₂называется линией центров или межосевым расстоянием — a_w.

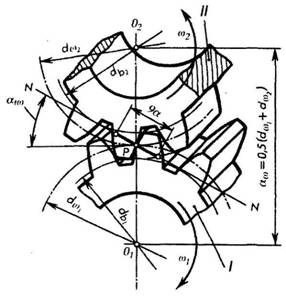
Рис. 16.2 – Пара колес в зацеплении

Точка Р касания начальных окружностей d_W1 и d_W2 — полюс — все­гда лежит на линии центров. Начальными называются окружнос­ти, касающиеся друг друга в полюсе зацепления, имеющие общие с зуб­чатыми колесами центры и перекатывающиеся одна по другой без сколь­жения.

Если проследить за движением пары зубьев двух колес с момен­та, когда они впервые коснутся друг друга до момента, когда они выйдут из зацепления, то ока­жется, что все точки касания их в процессе движения будут лежать на одной прямой NN. Прямая NN, проходящая через полюс за­цепление Р и касательная к ос­новным окружностям db₁, db₂, двух сопряженных колес, назы­вается линией зацепле­ния. Отрезок g_a линии зацепле­ния, отсекаемый окружностями выступов сопряженных колес, — активная часть линии зацепле­ния, определяющая начало и ко­нец зацепления пары сопряжен­ных зубьев.

Линия зацепления представ­ляет собой линию давления со­пряженных профилей зубьев в процессе эксплуатации зубча­той передачи.

Угол α между линией зацеп­ления и перпендикуляром к ли­нии центров O₁О₂ называется углом зацепления. В основу профилирования эвольвентных зубьев и инструмента для их на­резания положен стандартный по ГОСТ 13755-81 исходный контур так называемой рейки, равный 20°.

 Во время работы цилиндри­ческой прямозубой передачи сила давления Р_n ведущей шес­терни O₁ в начале зацепления передается ножкой зуба на со­пряженную боковую поверх­ность (контактную линию) головки ведомого колеса О₂. Чем больше пара зубьев одновременно находится в зацеплении, тем более плавно работает передача, тем меньшую нагрузку воспринимает на себя каждый зуб.

Стремление сделать зубчатую передачу более компактной вызывает не­обходимость применять зубчатые колеса с возможно меньшим числом зубь­ев. Изменение количества зубьев зубчатого колеса влияет на их форму. При увеличе­нии числа зубьев до бесконечно­сти колесо превращается в рейку и зуб приобретает пря­молинейное очертание. С умень­шением числа зубьев одновре­менно уменьшается толщина зу­ба у основания и вершины, а так­же увеличивается кривизна эвольвентного профиля, что приводит к уменьшению проч­ности зуба на изгиб. При умень­шении числа зубьев, когда z < z_mim, происходит так называе­мое подрезание зубьев, то есть явление, когда зубья большого колеса при вращении заходят в область ножки меньшего колеса (см. заштрихованная площадь на рис. 16.3), тем самым ослабляя зуб в самом опасном сечении, увеличивая износ зубьев и снижая КПД передачи.

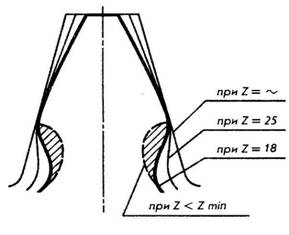
Рис. 16.3 – Подрезание зубьев

На практике подрезку зубьев предотвращают прежде всего выбором со­ответствующего числа зубьев. Наименьшее число зубьев (z_min), при кото­ром еще не происходит подрезание, рекомендуется выбирать от 35 до 40 при равном 15° и от 18 до 25 при α равном 20°.

В отдельных случаях приходится выполнять передачу с числом зубьев меньшим, чем рекомендуется, при этом производят исправление, или, как говорят, корригирование формы зубьев. Один из таких способов заключает­ся в изменении высоты головки и ножки зуба до h_a = 0,8m; h_f = m. Этот спо­соб исключает подрезку, но увеличивает износ зубьев.