14.12.Геометрические параметры зубчатого зацепления

Основные геометрические параметры зубчатого зацепления, представленные в таблице 14.5 и на рис. 14.3.

Таблица 14.5. Геометрические параметры зубчатого зацепления

Наименование параметра	Обозначение параметра	Расчетная формула
Модуль зацепления, мм	m	-
Число зубьев	z	-
Диаметр делительной окружности	d	d = m∙z
Диаметр окружности выступов, мм	da	da = d+2∙ha ha = m
Диаметр окружности впадин, мм	df	df = d-2∙hf
Высота ножки, мм	hf	hf = (1+С) ∙m C=0,5
Высота зуба, мм	h	h = ha+ hf
Окружной шаг, мм	р	р = π∙m
Толщина зуба, мм	s	s = p/2
Толщина впадины, мм	l	l = p/2
Ширина зуба, мм	b	b1 = b2+2∙m b2 = ψm∙m = 3
Межосевое расстояние, мм	aw	aw = m∙(z1+z2)/2

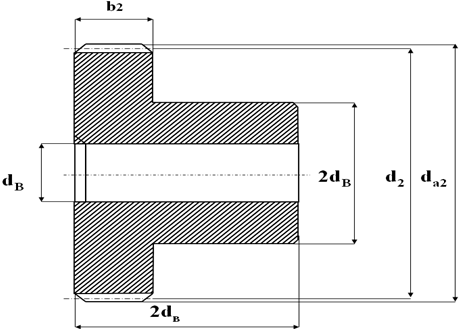
Рис. 14.3 – Эскиз зубчатого колеса.

14.13.Выбор подшипников по номинальному минимальному диаметру вала

Подшипник—изделие, являющееся частью опоры или упора, которое поддерживает вал, ось или иную подвижную конструкцию с заданной жёсткостью. Фиксирует положение в пространстве, обеспечивает вращение, качение или линейное перемещение (для линейных подшипников) с наименьшим сопротивлением, воспринимает и передаёт нагрузку от подвижного узла на другие части конструкции. Внешний вид подшипника качения представлен на рис. 14.6.

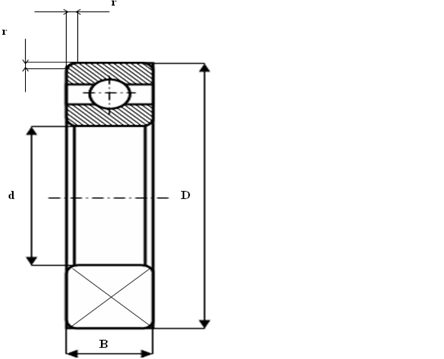
Рис. 14.6 – Изображение подшипников качения на чертежах

Расчете минимального диаметра вала:

, (14.23)

где [τ] = 30-40 МПа.

14.14.Проектный расчет валов

Выбор и проверочный расчет подшипников качения. Исходные данные для расчета:

Крутящие моменты:

Т₁ = 0,01 Нм;

Т₂ = 0,02 Нм;

Т₃ = 0,039 Нм;

Т₄ = 0,078 Нм;

Т₅ = 0,156 Нм.

Ширина зуба на колесе:

b_k = 4 мм;

Диаметр делительной окружности колеса:

d_k = 14 мм;

Соотношение максимального и номинального крутящих моментов выбранного электродвигателя:

Т_max/ Т_ном = 1,5.

Для проверочного расчета проверим последний вал, так как он самый нагруженный, схема представлена на рис 14.7.

Рис 14.7 – Конструктивная схема последней ступени зубчатого механизма

Для расчета построим расчетную схему вала, отметив все силы и реакции опор, действующие на последний вал. Итог показан на рис. 14.8.

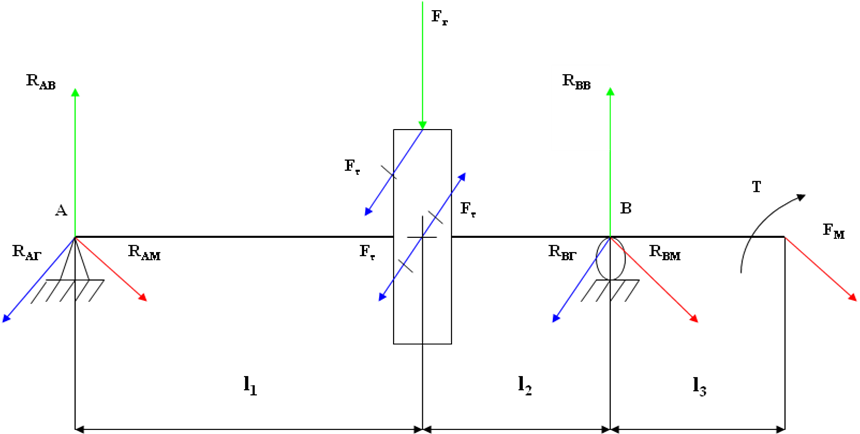
Рис. 14.8 – Расчетная схема вала.

Определяем внешние силы, приложенные к валу. На вал действует окружная сила, радиальная сила и усилие от действия муфты.

Окружная сила на валу последнего колеса:

Fτ = 2∙Т_а+1/ d_а+1 (14.24)

Радиальная сила равна:

Fr = Fτ∙tgα (14.25)

где α – угол зацепления.

Усилие от действия муфты:

Fм = 0,3∙Fτ. (14.26)

Определение длин участков для расчетной схемы вала:

L₁ = B/2 + a + l + a + (l - b_k/2) (14.27)

L₂ = b_k/2 + a + B/2; (14.28)

L₃ = B/2 + (a + 1) + l + a (14.29)

где a = 2 мм – торцевой зазор, B– ширина подшипника.

Определим опорные реакции от действующих на вал сил в горизонтальной плоскости (рис 14.9), в вертикальной плоскости (рис 14.10) и опорные реакции от муфт (рис 14.11).

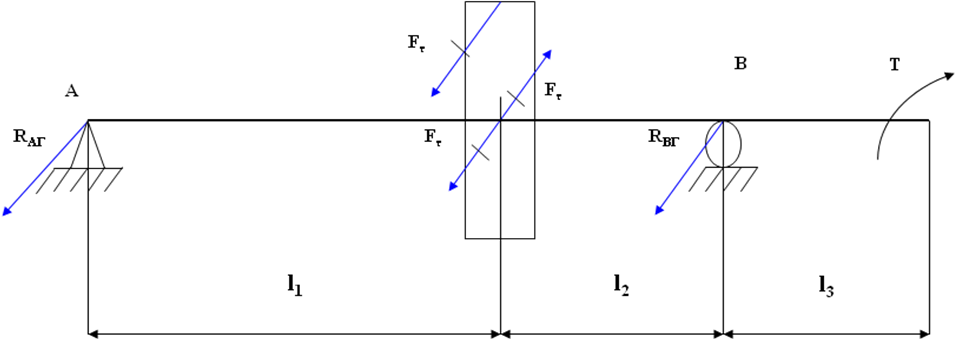
Рис 14.9 – Опорных реакций в горизонтальной плоскости.

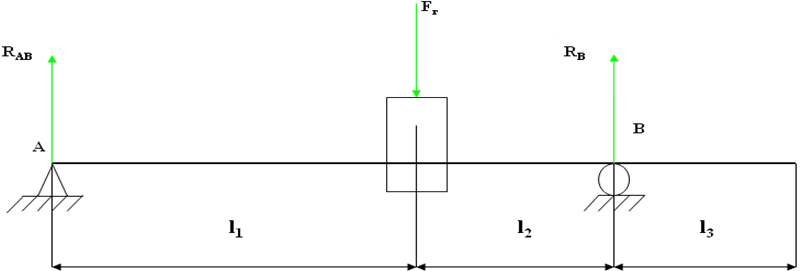
Рис 14.10 – Опорных реакций в вертикальной плоскости.

Рис 14.11 – Опорные реакции от муфт.

Определяем суммарные опорные реакции по правилу параллелограмма:

(14.30)

(14.31)

.