12.Разреженные матрицы в fem-анализе

Разреженные матрицы

Матрицы, в которых большинство элементов равно нулю, называются разреженными. Элементы матрицы - образуют главную диагональ; элементы матрицы образуют (k-1)-ую наддиагональ; элементы образуют (k-1)-ую поддиагональ.

Пример. Ниже представлены две матрицы: матрица A - трехдиагональная матрица размера 5х5, элементы главной диагонали равны 10, элементы первой наддиагонали равны 3, элементы первой поддиагонали равны -1 ; матрица В - симметричная матрица размера 5х5, на главной диагонали которой все элементы равны 10, на второй наддиагонали элементы равны 5, а на третьей наддиагонали элементы равны 2.

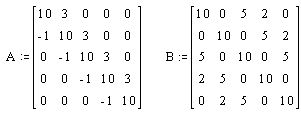
Форматы хранения разреженных матриц

В настоящее время во многих областях науки и техники многие расчеты ведутся с помощью систем линейных алгебраических уравнений (СЛАУ), причем матрица коэффициентов системы оказывается очень разреженной. Пример из электротехники: для расчета схемы, состоящей из 68 элементов, составляется матрица, разреженность которой составляет 0.085, т.е. отношение ненулевых элементов матрицы ко всем ее элементам равняется именно этому числу. Назрела необходимость найти быстрый и эффективный по затратам памяти способ решения СЛАУ с большим количеством ненулевых элементов. Ведь хранить полностью в памяти разреженную матрицу и тратить время на операции над нулевыми элементами слишком разорительно.

Динамический формат хранения разреженных матриц

В основе динамического формата лежит использование хэш-таблицы, что позволяет осуществлять быстрый доступ к элементу матрицы по его индексу. Вставка элемента в матрицу может потребовать несколько больше времени, особенно если потребуется увеличивать хэш-таблицу в связи с её заполнением. Помимо добавления элемента и доступа к элементу есть и другие операции, в частности - получение списка элементов, расположенных в некоторой строке или столбце. Хэш-таблица сама по себе не подходит для подобных операций (потребовалось бы просмотреть всю таблицу для составления подобного списка), поэтому для эффективного доступа к строке/столбцу используется ортогональный односвязный список, т.е. односвязный список, в котором каждый элемент матрицы связан с двумя соседями - соседом справа и соседом снизу. Такой список позволяет с минимальными затратами пройти по строке или столбцу. В сочетании эти две структуры данных порождают структуру, в которой элемент является одновременно и частью хэш-таблицы, и частью ортогонального списка.

Динамический формат неплохо подходит для начального заполнения матрицы, поскольку он позволяет не беспокоиться о таких вещах, как предварительное выделение памяти. От программиста требуется только задавать значения элементов матрицы, а требуемая память будет выделена автоматически. Вместе с тем, этот формат характеризуется значительными накладными расходами на хранение элементов. В случае, если матрица имеет очень большой размер, сравнимый с размером оперативной памяти компьютера, имеет смысл создавать матрицу сразу в статическом формате хранения при помощи соответствующей функции.

Статический формат хранения разреженных матриц

В основе статического формата хранения разреженной матрицы лежит представление матрицы в виде списка индексов ненулевых элементов и соответствующих им значений, упорядоченного по строкам. Такое представление позволяет эффективно осуществлять умножение разреженной матрицы на вектор/матрицу, а также просматривать разреженную матрицу по строкам. Вместе с тем, модификация матрицы, представленной в этом формате, невозможна из-за высокой трудоемкости, некоторые другие операции также требуют больших трудозатрат.

МКЭ и СЛАУ

В настоящее время в связи с бурным развитием информационных технологий и САПР в машиностроении широкое распространение получили компьютерные системы инженерного анализа, имеющие разнообразную теоретическую и прикладную направленность. Рядовой пользователь проводит, например, расчет прочности или температурных полей в конструкции через интерфейс компьютерной программы, но должен иметь представление о структуре компьютерных вычислений, чтобы грамотно выбирать настройки генерации расчетной сетки и решателя.

Наиболее эффективный численный метод решения инженерных задач при компьютерном проектировании - метод конечных элементов (МКЭ). Он позволяет преобразовать аналитические уравнения математической модели к тому виду, который непосредственно обрабатывается компьютером. В процессе построения дискретных эквивалентов дифференциальных уравнений, описывающих физические процессы проектируемых инженерных систем, возникают большие системы линейных, а в общем случае нелинейных, алгебраических уравнений. Для этого в каждом расчетном узле производные исходного дифференциального уравнения записываются в виде конечной разности искомых параметров между соседними шагами в пространстве или во времени. Нелинейные задачи возникают, например, когда коэффициенты дифференциальных уравнений, отражающие свойства материалов или среды, сами являются функцией искомого параметра.

Нелинейные системы уравнений решаются в два этапа: на первом этапе они линеаризуются, а затем полученная система линейных уравнений на каждом шаге решается с помощью какого-либо метода линейной алгебры. Если сходимость не достигнута, то процесс повторяется. Таким образом, каждый раз решается система линейных алгебраических уравнений (СЛАУ):

[A]{u}={f} (*)

где {u} — вектор искомых узловых параметров; {f} — вектор нагружения.

Матрицы [A] СЛАУ (*), как правило, симметричны и имеют выраженную разреженную структуру, т.е. содержат большое количество нулевых элементов. Выбрав определенную нумерацию узлов расчетной сетки, эти матрицы можно привести к ленточной структуре, когда ненулевые элементы собраны вблизи главной диагонали матрицы. Для ленточных матриц вводят понятие "ширины ленты" - это количество ненулевых элементов строки вблизи главной диагонали.

При использовании конечно-элементной технологии возникает проблема разработки эффективных алгоритмов формирования, хранения и использования разреженных матриц. Память, используемая для хранения разреженных матриц, состоит из двух частей: основной памяти, в которой содержатся числовые значения элементов матриц, и дополнительной памяти, где хранятся указатели, индексы и другая информация, необходимая для формирования структуры матриц и обеспечивающая доступ к числовым значениям их элементов при выполнении процедур формирования и решении СЛАУ, т. е. так называемые списки связности. Способы хранения и использования данных, хранящихся в основной и дополнительной памяти, весьма разнообразны и определяются, главным образом, выбранным методом решения СЛАУ.

При реализации итерационного решения системы уравнений (*) весьма частой является ситуация, когда необходимо выполнить умножение матрицы системы [A] на какой-либо вектор, например, на вектор узловых неизвестных {u} или на вектор невязки {r}. Построение произведений типа [A]{u} или [A]{r} является одним из узких мест эффективной реализации всего итерационного процесса решения системы уравнений (*), поскольку требует наибольших затрат процессорного времени.

Решение СЛАУ методом сопряженных градиентов

Метод сопряженных градиентов - это наиболее популярный метод для решения системы линейных уравнений с разреженной симметричной положительно определенной матрицей. Алгоритм обладает тремя притягательными чертами. Во-первых, он использует только операцию умножения матрицы системы на вектор, т.е. может применяться как для решения задач, в которых матрица системы задана в явной форме, так и для решения задач, в которых матрица доступна только через операцию умножения на вектор. Во-вторых, алгоритм требует фиксированного времени на каждую итерацию, независимо от числа осуществленных итераций (в некоторых алгоритмах это условие не выполняется). Третьим достоинством является то, что алгоритм всегда сходится.

Метод сопряженных градиентов является одним из методов подпространств Крылова, т.е. методов, строящих ортогональный базис подпространства span{ r₀ , Ar₀ , A ²r₀ , ..., A ⁱr₀ } для некоторого стартового вектора r₀  . Решение исходной системы Ax = b ищется на этом подпространстве путем минимизации невязки. Два свойства алгоритма, отмеченные выше, вытекают из того, что для построения ортогонального базиса используются последовательное умножение стартового вектора на матрицу A и трехчленные рекуррентные соотношения для ортогонализации генерируемых векторов (отсюда постоянные затраты на одну итерацию - каждый новый вектор ортогонализируется путем операций только с двумя предыдущими векторами).