8.Введение в мкэ

Итак, мы выяснили, что существует достаточно универсальный численный метод конечных элементов (МКЭ), который эффективно можно использовать для расчетов деформаций консервных банок, автомобилей и многого другого. Надо понять, как этот метод работает. Более плотное знакомство с МКЭ мы проведем в достаточно простой форме, не углубляясь в дебри, а лишь обозначая некоторые важные проблемы.

Итак, пусть есть абстрактная задача найти некоторую зависимость y от x в интервале от a до b. Можно поступить двояко:

1) искать аналитический вид зависимости в виде функции y=y(x), т.е. в виде некоторой формулы, как например, все делали в школе, когда брали интеграл, или

2) искать функцию в виде набора точек с некоторой нужной или заданной точностью.

Рис. 8.9- Аппроксимация функции ломаной

Так, например, на Рис. 8 .9 показана некоторая искомая функция y=y(x), вместо которой найдена ломаная 1-2-3-4-5-6 без особого ущерба для точности. Понятно, что чем в большем числе точек искать значение функции, тем точнее будет результат ее представления ломаной. А методы, которые вместо аналитической зависимости находят искомую функцию (или много функций) в виде конечного числа точек (чисел), называются численными.

Наберемся терпения и решим простую, но реальную задачу. Пусть требуется сделать расчет упругого изгиба некоторого элемента конструкции с первоначальной прямой формой, один из концов которого жестко закреплен, а другой конец отогнут вниз под действием некоторой силы, как показано на рисунке ниже. Таким элементом конструкции может быть консольная балка, стойка и т.п.

Рис. 8.10 - Балка, состоящая из двух конечных элементов.

Для определенности на Рис. 8 .10 наша балка уже разбита (представлена) в виде двух (не будем усложнять) конечных элементов, первый из которых имеет узлы 1 и 2, а второй – узлы 2 и 3. Т.е. узел 2 является общим для соседних конечных элементов.

Но прежде чем начать решать конкретную задачу, надо уяснить свойства конечного элемента в общем виде. Рассмотрим абстрактный конечный элемент с узлами i и j (Рис. 8 .11).

Рис. 8.11 - Конечный элемент

Конечным элементом будем называть такую часть элемента конструкции, чтобы перемещения любой его точки можно было бы выразить через перемещения его узлов без значительного ущерба для точности решения. При изгибе каждая точка конечного элемента с узлами ij имеет две степени свободы:

1) точка может перемещаться по вертикали на расстояние v, 

2) поперечное сечение в точке может развернуться на некоторый угол Ө . 

Так как конечный элемент представлен двумя узлами, то он имеет четыре степени свободы. Значит, функцию перемещения в каждой точке с координатой x внутри элемента можно представить полиномом с четырьмя коэффициентами

.

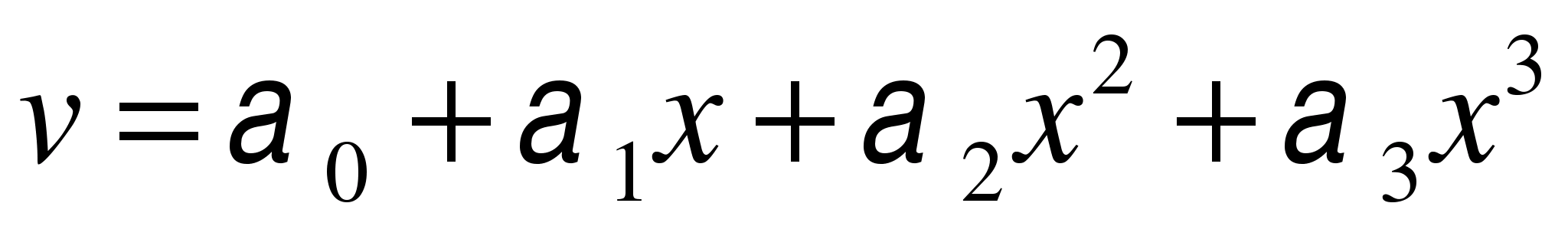Возникает вопрос, а почему полиномом, ведь истинная функция перемещения может быть сколь угодно сложной? Ответ – так проще. Мы же представили полиномом первой степени (отрезком прямой) функцию y(x) внутри каждого конечного элемента, что было показано на рисунке, и убедились, что точность достаточна. А если нужна точность больше, то всегда можно увеличить количество конечных элементов.

Известно (например, из сопромата), что функция угла разворота сечения есть первая производная от функции перемещения, т.е.

.

Положим, что начало системы координат расположено в узле i конечного элемента, а координатная ось x направлена вправо. Тогда выразим коэффициенты полинома через перемещения узлов i и j, т.е. v_i, Ө_i, v_j и Ө_j.

При x=0, т.е. в узле i

В узле j, т.е. при x=x_j=l, где l=x_j-x_i – длина конечного элемента, и с учетом полученных выше значений и

Решая эту систему уравнений, окончательно получаем

Подставляя полученные выражения для в формулу для v, получаем

Выглядит громоздко, но результат получен – мы выразили перемещение в любой точке конечного элемента через перемещения в его узлах – основных неизвестных задачи, так как, разбивая конструкцию на конечные элементы, мы и сбирались вычислять искомую функцию перемещений лишь в некоторых точках, а между ними представлять ее приближенно (аппроксимируя). Теперь, зная длину элемента l, перемещения в узлах конечного элемента v_i,Ө_i,v_j,Ө_j и координату какой-либо точки x мы можем по этой формуле найти перемещение этой точки v.

Громоздкую запись последней формулы можно устранить, записав ее в матричном виде. Введем вектор узловых перемещений конечного элемента в виде

.

Введем вектор формы элемента в виде

.

Тогда выражение для перемещения v можно компактно записать в виде

,

где верхний индекс Т обозначает операцию транспонирования матрицы.

Далее следует договориться, что имеется в виду под словом «деформация». В английском языке русскому слову «деформация» соответствуют два несколько разных понятия – deformation и strain. Первое из них обозначает изменение геометрии чего-либо, т.е. то же самое, что и русское слово «деформация», применяемое в разговорном языке. Это – обобщенное понятие для растяжения, сжатия, скручивания, изгиба, смятия и т.п. Английское же слово strain обозначает меру деформации, или степень деформации.

Рассмотрим, например, образец из какого-либо материала с начальной длиной L₀. Если этот образец, например, растянуть, т.е. увеличить его длину на величину до длины , то степенью деформации будем называть безразмерную величину

.

Величину и будем называть деформацией, или относительной деформацией. Недостатком относительной деформации является то, что она не аддитивна – при сложении относительных деформаций накапливается ошибка. Например, образец длиной 10см некий экспериментатор растянул на 1см, т.е. получил деформацию =1/10. Теперь наш образец имеет длину 11см. Другой экспериментатор, не зная о прошлой истории образца, растянул его еще на 1см, т.е. получил деформацию =1/11. Но тогда суммарная относительная деформация равна

,

что явно меньше деформации =2/10, полученной этим образцом изначально. Выход из этой ситуации есть, но для нашей задачи оставим прежнее определение относительной деформации, которое можно корректно использовать для малых деформаций.

Рис. 8.12 - Состояние до и после изгиба

Наша конструкция имеет некоторую толщину, пусть постоянную по длине конечного элемента. Малый фрагмент элемента длиной dx до изгиба показан на Рис. 8 .12 слева, а после изгиба – справа. При изгибе некоторое материальное волокно (ось) АВ не изменит своей длины, т.е. АВ=А₁В₁, а радиус его кривизны составит . Относительная деформация произвольного волокна CD будет равна

откуда окончательно получаем

.

Из математики известна зависимость для малых величин углов разворота сечения

.

Тогда окончательно имеем

,

или

,

где вектор есть

.

Согласно закону Гука напряжения (силы на единицу сечения) связаны с деформациями через модуль упругости (модуль Юнга) E

.

Известно (из сопромата), что изгибающий момент связан с напряжениями в сечении, с учетом осевого момента инерции сечения, выражением

,

откуда получаем вектор узловых сил

.

Теперь мы имеем вектор узловых перемещений конечного элемента, вектор узловых сил конечного элемента, вектор относительных деформаций и вектор напряжений в сечении . При этом вектора , и выражаются через компоненты вектора , которые, напомним, являются неизвестными задачи.

Если к некоторому узлу (или узлам) сетки конечных элементов (конечно-элементному аналогу) приложить внешние силы или, что одно и то же, задать им некоторые перемещения, известные, например, из измерений деформации нашей конструкции, то истинные перемещения остальных узлов будут такими, которые обеспечивают минимум полной энергии деформации.

Минимизация полной энергии равносильна решению системы дифференциальных уравнений, описывающих деформацию балки.

Как же вычислить полную энергию? Произведение напряжений на соответствующие деформации дают удельную энергию деформации (на единицу объема). Чтобы вычислить энергию деформации по всему объему конечно-элементного аналога, надо проинтегрировать (просуммировать) удельную энергию деформации по объему конечного элемента и просуммировать по всем элементам конечно-элементного аналога. Далее, произведение узловых сил на соответствующие узловые перемещения дают работу внешних сил. Полная же энергия деформации есть разность энергии деформации всех конечных элементов конечно-элементного аналога с работой внешних сил. И чтобы найти ее минимум, надо записать выражение для полной энергии и продифференцировать его по каждому перемещению. Совокупность частных производных даст систему линейных уравнений в виде

,

где – матрица жесткости конечно-элементного аналога, – вектор узловых перемещений конечно-элементного аналога, – вектор узловых сил конечно-элементного аналога.

Вид последней формулы показывает, что энергия деформации конечно-элементного аналога равна работе внешних сил (работа внутренних сил рана работе внешних сил).

Не утомляя читателя выводом, сразу покажем, что выражение для матрицы жесткости конечного элемента следующее

.

Видно, что матрица жесткости конечного элемента имеет размер 4х4, и симметрична относительно главной диагонали. Используя обозначения узлов конечного элемента i и j, структуру этой матрицы можно представить в виде

,

где – подматрицы размером 2х2, а подстановка вместо i и j номеров узлов конечного элемента показывает место каждой подматрицы в глобальной матрице жесткости конечно-элементного аналога.

Аналогично структуру вектора перемещений и вектора узловых сил конечного элемента можно представить в виде двух подвекторов, а подстановка вместо i и j номеров узлов конечного элемента показывает место каждого подвектора в глобальном векторе узловых перемещений и узловых сил конечно-элементного аналога

.

Сейчас начнем решать реальную задачу в цифрах, и все станет окончательно понятно. Вновь обратимся к нашему второму рисунку. Пусть конечный элемент №1 имеет узлы 1 и 2 с координатами и мм. Пусть конечный элемент №2 имеет узлы 2 и 3 с координатами мм и мм, т.е. длина l=100мм одинакова для обоих конечных элементов. Для обоих конечных элемента примем модуль упругости кг/мм², осевой момент инерции сечения мм⁴ .

Вычисляем компоненты матрицы жесткости первого и второго конечных элементов, они будут одинаковы и равны

.

Далее распределяем подматрицы этих матриц по глобальной матрице жесткости в соответствии с номерами узлов, как показано на рисунке ниже, и суммируя

Получаем глобальную матрицу жесткости размером 6х6 в виде

.

Узловые силы пока не заданы, и глобальный вектор узловых сил заполнен нулями

.

Имея неизвестный глобальный вектор узловых перемещений

,

тем самым имеем систему линейных уравнений

,

решение которой пока тривиально, так как не заданы силы или перемещения, или, как обычно говорится в литературе, не заданы граничные условия. Возвращаясь ко второму рисунку видим, что в узле №1 имеет место жесткое закрепление балки, т.е. перемещение и угол разворота сечения там равны нулю, или и .  Поэтому обнуляем первую и вторую строки, и первый и второй столбцы матрицы жесткости, ставим на главные диагонали по 1. Получаем

.

Теперь из решения системы уравнений всегда будет и .

Зададим перемещение узла №3 вниз на 10мм, или . Для этого сформируем некоторый вектор в виде

,

и получим измененный вектор по алгоритму

,

т.е. вычтем из вектора произведение , а результат поместим снова в вектор . Теперь вектор выглядит как

.

Обнулим пятую строку и пятый столбец матрицы , поставим в главной диагонали на пятой строке 1, поставим в векторе на пятой строке -10. Граничное условие внесено, а матрица и вектор теперь выглядят как

,

и

.

Теперь можно решать систему уравнений. Тогда решение есть

,

или , , мм, рад, мм, рад.

Ну и теперь, когда узловые перемещения найдены, можно подставить из в формулу для перемещения v и построить его график – форму деформированной балки (Рис. 8 .13).

Рис. 8.13 - Форма деформированной балки

С аналитическим решением можно не сравнивать – совпадение будет на все 100%, так как реально упругая линия балки описывается уравнением третьей степени.

В результате преобразований исходной системы уравнений у нас фактически осталось только три неизвестных – перемещение и угол разворота сечения в узле №2, и угол разворота сечения в узле №3. В результате решения эти неизвестные найдены такими, что обеспечивают минимум затрат энергии на деформацию – любая иная их комбинация приведет к росту затраченной энергии.