62. Проверка статистическим методом однородности дисперсий серии измерений

Однородными сериями измерений называются такие, у которых вероятности результатов измерений подчиняются одному закону. На практике однородными считают такие серии измерений, у которых числовые характеристики законов распределения вероятности (ЗРВ)   и   отличаются случайным образом.Что касается дисперсий, то уместнее говорить не об их равенстве, а об однородности, то есть о случайном (незначимом) различии. Как указывалось ранее, проверка неоднородности дисперсий позволяет определить методику дальнейшей обработки результатов измерений. Если дисперсии однородны, то обработка результатов ведется по схеме равноточных серий измерений, если же дисперсии неоднородны, то обработка результатов ведется по схеме неравноточных серий измерений.

Проверку однородности дисперсии опытов при различных сочетаниях уровней факторов наиболее просто можно осуществить путем сравнения наибольшей и наименьшей дисперсии опытов по критерию Фишера:

где F_р - расчетное значение критерия Фишера, - наибольшая и наименьшая дисперсии из всех серий.

Если полученное расчетом значение критерия Фишера меньше табличного для соответствущих чисел степеней свободы при принятом в технике уровне значимости 5%, то дисперсии опытов однородны. Если полученное расчетом критерий Фишера больше табличного не более чем в два раза, то необходимо проверить однородность дисперсии всех опытов более точным расчетом ро критерию Кохрена или по критерию Бартлета.

63. Проверка статистическим методом значимости коэффициентов уравнения регрессии.

Проверка значимости коэффициентов в уравнении регрессии производят следующим образом. Вначале определяют дисперсию значений коэффициентов уравнения при равном числе параллельных опытов (при неравномерном дублировании опытов формула служит для приближенной оценки)

где n – число параллельных опытов.

Затем определяют доверительный интервал Δb для значений коэффициентов по выражению

где t – табличное значение критерия Стьюдента при принятом уровне значимости 5% и числе степеней свободы, с которым определялась дисперсия .

Коэффициент значим, если его абсалютн7ая величина больше доверительного интервала. В противном случае коэффициент незначим и слагаемое, в которое он входит, можно исключить из интервала.

64. Проверка статическим методом адекватность математической модели.

Цель планирования экспериментов - получение математической модели, адекватной наблюдаемому явлению с заданной точностью и с минимальными затратами. Математическая модель является информационным отражением или реальных процессов, или абстрактных схем.

Проверку адекватности математичесокй модели проводят с использованием критерия F, который рассчитывается по выражению

где - дисперсия адекватности.

Дисперсию адекватности при одинаковых и неодинаковых числах параллельных опытов вычисляют соответственно по формулам:

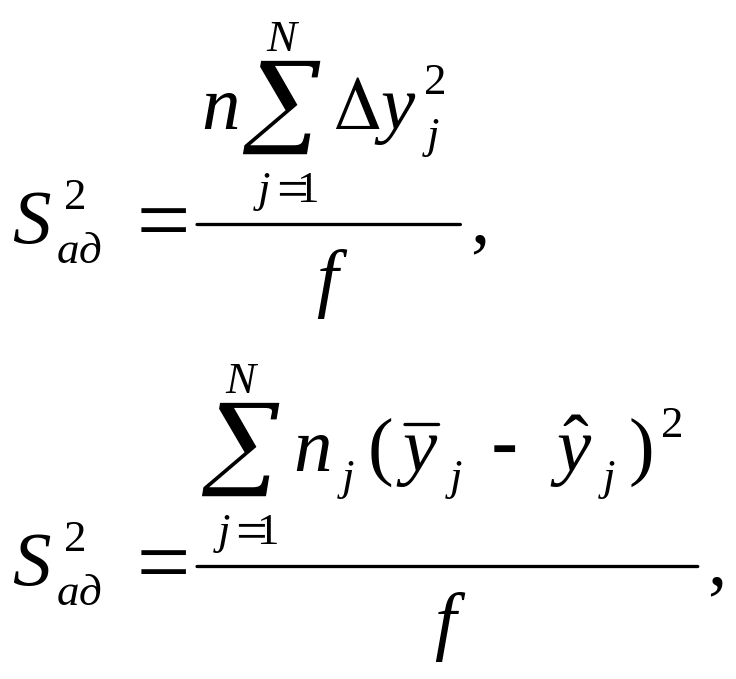
где nj – число параллельных j-ых опытов;

= - разность между вычисленным по модели значением парамтра оптимизиции и полученным в j-м опыте;

- среднее значение параметра оптимизиции из параллельных опытов;

- значение параметра оптимизации, вычисленной по модели;

f - число степеней свободы для линейной модели.

При вычислении значения факторов необходимо подставить в кодированном виде. Если расчетное значение критерия Фишера меньше табличного, модель считается адекватной.

Если модель не адекватна данным эксперимента, то необходимо перейти к более сложной формуле уравнения регрессии или уменьшить интервал варьирования, проводя повторные опыты.