16. Плотность распределения

Непрерывную случайную величину можно задать не только интегральной функцией распределения, но и дифференциальной функцией. Рассмотрим эту форму задания распределения случайной величины. Пусть задана непрерывная случайная величина Х с функцией распределения . Тогда, если существует , то функция называется дифференциальной функцией распределения или плотностью распределения.

Используя методы интегрального исчисления, можно предложить формулу для нахождения интегральной функции распределения по плотности .

Свойства плотности распределения.

1. Плотность распределения больше либо равна нулю для любого значения аргумента, то есть . Так как интегральная функция распределения неубывающая, следовательно, её производная неотрицательная.

2. Вероятность попадания случайной величины в заданный интервал находится по формуле .

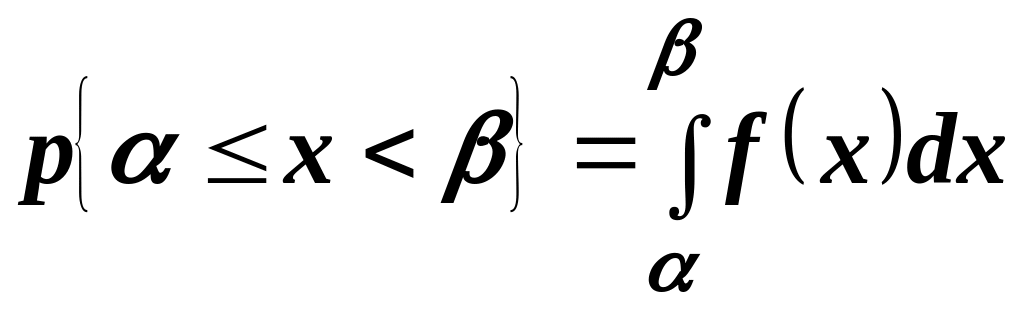3. Условие нормировки. Интеграл в бесконечных пределах от плотности распределения равен единице, .

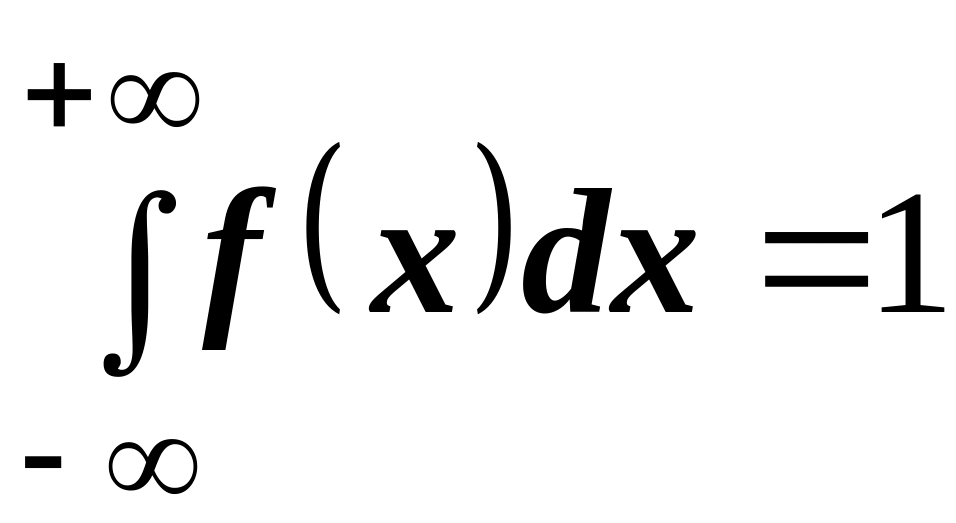Пример 20. Случайная величина Х подчинена закону распределения с плотностью .

Определить коэффициент с. Найти вероятность попадания случайной величины на участок от 0 до и функцию распределения.

Решение. Площадь, ограниченная кривой распределения, равна , по условию нормировки получаем . Вероятность попадания в интервал найдём по формуле

.

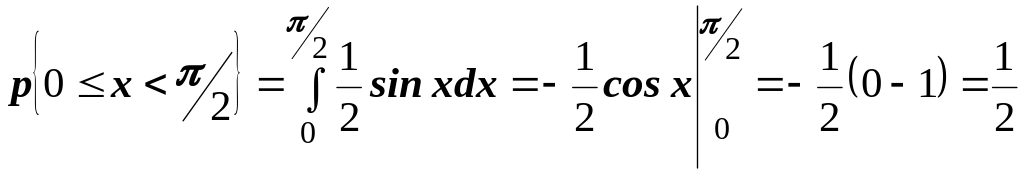Интегральную функцию распределения найдём по формуле . Для : имеем .

Для :

.

Для : .

Следовательно, интегральная функция распределения имеет вид

17. Математическое ожидание

Математическое ожидание определяет положение случайной величины на числовой оси, показывая центр распределения (некоторое среднее значение, около которого сосредоточены все возможные значения случайной величины).

О. 1. Математическим ожиданием дискретной случайной величины называют сумму произведений всех возможных значений на их вероятности, то есть .

О. 2. Математическое ожидание непрерывной случайной величины Х , возможные значения которой принадлежат интервалу , находится по формуле .

Основные свойства математического ожидания.

1. Математическое ожидание постоянной равно самой постоянной, .

2. Постоянный множитель выносится за знак математического ожидания, .

3. Математическое ожидание суммы двух случайных величин равно сумме их математических ожиданий, .

4. Математическое ожидание произведения двух независимых случайных величин равно произведению их математических ожиданий, .

5. Математическое ожидание отклонения случайной величины от её математического ожидания равно нулю, .

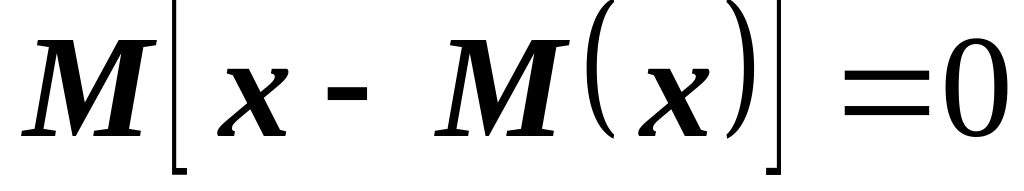Пример 21. Найти математическое ожидание для случайной величины, заданной функцией распределения:

Решение. Найдём плотность распределения из соотношения

Математическое ожидание непрерывной случайной величины находим по формуле

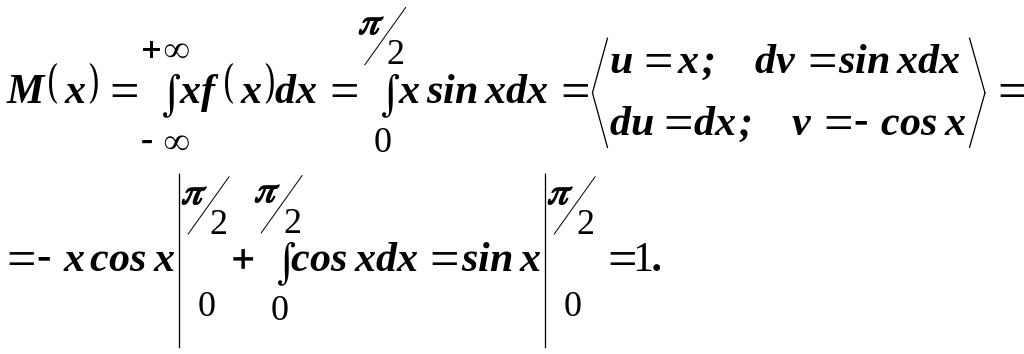Пример 22. Найти математическое ожидание для ряда

xi	0	1	2	3
pi	0,1	0,3	0,4	0,5

распределения

Решение. Для дискретной случайной величины используем формулу .

О.3. Модой М₀ дискретной случайной величины называется её значение, имеющее наибольшую вероятность.

О.4. Модой М₀ непрерывной случайной величины называется такое её значение, при котором плотность распределения имеет максимум.

Геометрически моду можно интерпретировать как абсциссу точки максимума кривой распределения. Бывают двухмодальные и многомодальные распределения. Встречаются распределения, которые имеют минимум, но не имеют максимума. Такие распределения называются антимодальными.

О.5. Медианой случайной величины М_е называют такое её значение, для которого справедливо равенство , то есть равновероятно, что случайная величина окажется больше или меньше медианы.

С геометрической точки зрения, медиана – абсцисса точки, в которой площадь, ограниченная кривой распределения, делится пополам. Так как вся площадь, ограниченная кривой распределения и осью абсцисс, равна единице, то функция распределения в точке, соответствующей медиане, равна 0,5:

.