4. Геометрическая вероятность

О. 1. Геометрической вероятностью события А называется отношение меры области благоприятных исходов к мере области всевозможных исходов.

В частности, для плоскости согласно определению , где - площадь области благоприятных исходов, - площадь области всевозможных исходов.

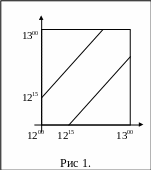Пример 7. (Задача о встрече) Два студента условились встретиться в определённом месте между 12 и 13 часами. Пришедший первым ждёт второго в течение 15 минут, после чего уходит. Найти вероятность того, что встреча состоится, если каждый студент наудачу выбирает момент своего прихода (в промежутке от 12 до 13 часов).

Решение. Обозначим событие А – студенты встретятся, тогда противоположное событие - студенты не встретятся. Отложим по оси Ох время прихода первого студента, по оси Оу время прихода второго студента. Тогда точка области с координатами однозначно определяет время прихода обоих студентов. Студенты встретятся, если выполнено условие . Построим две прямые линии и . Область, заключённая между этими линиями внутри квадрата, составляет область благоприятных исходов события А Рис. 1. Для события область благоприятных исходов согласно Рис. 1 состоит из двух прямоугольных треугольников с катетами, равными , общей площадью, равной . Область всевозможных исходов равна площади квадрата со стороной 1. Следовательно, площадь всевозможных исходов равна . Тогда вероятность события равна . Поэтому искомая вероятность равна .

5. Теоремы сложения

Т.1. Для несовместных событий вероятность появления суммы событий равна сумме вероятностей. То есть .

Доказательство. Пусть опыт имеет n исходов, событию А благоприятствует k из них, а событию В - благоприятствует m. Тогда сумме событий А+В благоприятствуют m+k. Тогда

.

Пример 8. Вероятности получить на экзамене 5, 4, 3 соответственно равны 0,2; 0,3; 0,3. Найти вероятность успешной сдачи экзамена.

Решение. Обозначим события А – студент успешно сдал экзамен; В; С; К – студент сдал экзамен на 5; 4; 3 соответственно. По условию . В силу несовместности событий В; С; К и по условию по теореме имеем .

Т. 2. Для любых событий вероятность появления суммы этих событий равна сумме вероятностей этих событий без вероятности их совместного появления. То есть .

Доказательство. Представим сумму событий А+В в виде суммы несовместных событий , а событие В в следующем виде . Так как в обоих случаях события несовместны, то, применяя первую теорему, имеем ; , из второго равенства получаем . Подставляя в первое, получаем окончательно .

6. Теоремы умножения

О. 1. Два события называются независимыми, если вероятность появления одного из них не зависит от того, произошло или не произошло второе событие.

О. 2. Несколько событий называются независимыми в совокупности, если любая комбинация из них независима.

О. 3. События называются зависимыми, если появление или не появление одного из них, изменяет вероятность появления другого.

О. 4. Вероятность события В, вычисленная в предположении осуществления события А, называется условной вероятностью события В и обозначается .

Пример 9. Из урны, содержащей 2 белых и 3 чёрных шара, наудачу последовательно извлекают два шара. Найти вероятность того, что второй извлечённый шар белый если известно, что первый извлечённый шар чёрный.

Решение. Обозначим события А – первый извлечённый шар чёрный, В - второй извлечённый шар белый. Для нахождения искомой вероятности используем классическое определение , где m- число благоприятных исходов, равное числу оставшихся после первого извлечения белых шаров, то есть m=2, а n- число всевозможных оставшихся шаров, то есть n=4. Тогда искомая вероятность равна .

Т. 1. Вероятность произведения двух событий равна произведению вероятности одного из них на условную вероятность другого, вычисленную при условии, что первое событие произошло. То есть .

Доказательство. Пусть число всевозможных исходов опыта равно n. Из них событию А благоприятствует m из них. Совместному появлению событий А и В благоприятствует k. Тогда , так как число всевозможных исходов для этого условного события равно m (событие А произошло), число благоприятных исходов равно k (событие В происходит при условии появления события А). Для других вероятностей имеем . Подставляя в формулу, имеем тождество.

Следствие 1. Если появление события А не зависит от события В, то появление события В не зависит от события А.

Доказательство. Если появление события А не зависит от события В, то можно записать . Используя две записи теоремы умножения, имеем, подставив указанное условие, получим , разделив обе части на , получим , то есть вероятность появления события В не зависит от события А.

Следствие 2. Вероятность произведения двух независимых событий равна произведению вероятности этих событий.

Доказательство. Применяя первое следствие к теореме умножения, получаем .

Пример 10. Известно, что 85% готовой продукции цеха является стандартной. Вероятность того, что стандартная деталь отличного качества, равна 0,51. Найти вероятность того, что наудачу взятое изделие окажется отличного качества.

Решение. Пусть А- событие, означающее, что взятое наудачу изделие стандартное, В- событие, означающее, что изделие отличного качества. Изделие может быть отличного качества, если оно стандартное. Поэтому из условия задачи следует . Тогда искомая вероятность равна .