1. Источники финансирования системы здравоохранения в современных условиях.

До перехода на медицинское страхование существовало жесткое бюджетное финансирование, не отвечающее повышенным потребностям населения. В связи с внедрением принципов медицинского страхования в стране была практически пересмотрена система финансирования как отрасли в целом, так и отдельных медицинских учреждений. В настоящее время источниками финансовых ресурсов системы здравоохранения являются: 1. Бюджетные средства - средства федерального бюджета, бюджетов республик в составе РФ и местных бюджетов, т.е. бюджетов всех уровней 2. Средства системы ОМС, поступающие от государственных и общественных организаций (объединений), предприятий и других хозяйствующих субъектов 3. Внебюджетные средства - средства добровольного медицинского страхования (ДМС), личные средства граждан, безвозмездные и (или) благотворительные взносы и пожертвования, доходы от ценных бумаг, кредиты банков и других кредиторов и др. Финансовые средства государственной и муниципальной систем здравоохранения. Средства государственной, муниципальной систем здравоохранения -это средства, поступающие из местных бюджетов и государственного бюджета в учреждения государственной системы здравоохранения. Перечень всех учреждений и мероприятий, финансируемых из бюджета, указан в «Программе государственных гарантий обеспечения граждан Российской Федерации бесплатной медицинской помощью» (26.10.2000г.). Из федерального бюджета финансируются все Федеральные центры и научно-исследовательские институты, федеральные реабилитационные центры, федеральные целевые программы («Вакщшо-профилактика», «Сахарный диабет», «Неотложные меры по борьбе с туберкулезом в России», «АнтиВИЧ/СПИД», «Дети России» и многие другие) Из бюджетов субъектов Федерации и муниципальных бюджетов финансируются: специализированные диспансеры: противотуберкулезные, психоневрологические, кожно-венерологические, наркологические и др. дома ребенка, детские санатории центры по профилактике и лечению СПИДа станции скорой медицинской помощи, переливания крови бюро судмедэкспертизы, патолого-анатомические бюро центры медицинской профилактики, врачебпо-физкультурные диспансеры; участковые больницы, фельдшерско-акушерские пункты хосписы, больницы сестринского ухода отделения экстренной медицинской помощи областных больниц (санитарная авиация); медицинская помощь при врожденных пороках развития профессиональная подготовка и переподготовка кадров; приобретение дорогостоящего медицинского оборудования; финансирование дорогостоящих видов диагностики и лечение научные исследования; бесплатное льготное обеспечение лекарствами граждан и др. К сожалению, государство не может обеспечить достойное бюджетное финансирование здравоохранения. В 2001 г. на здравоохранение было выделено около 4 % от ВНП (валового национального продукта), в то время как этот процент должен составлять не менее 10-12 %. Средства системы обязательного медицинского страхования. Средства системы обязательного медицинского страхования - это средства, поступающие из страховых медицинских организаций. Финансовые средства государственной системы обязательного медицинского страхования предназначены для реализации государственной политики в области обязательного медицинского страхования и формируются за счет отчислений страхователей на обязательное медицинское страхование. В большинстве зарубежных стран с развитой системой обязательного медицинского страхования существует три основных источника финансирования обязательного медицинского страхования: 1. Отчисления из бюджета 2. Средства предпринимателей 3. Личные средства граждан. В России финансовые средства системы обязательного медицинского страхования формируются из двух источников: 1. Платежи из бюджета 2. Отчисления предприятий, организаций и других юридических лиц в фонд обязательного медицинского страхования в размере 3,6% от начисленной заработной платы. Средства поступают через банки в фонды обязательного медицинского страхования от страхователей, которые обязаны в этих фондах зарегистрироваться в качестве плательщиков страховых взносов. Финансовые средства фондов обязательного медицинского страхования находятся в государственной собственности, не входят в состав бюджетов других фондов и изъятию на другие цели не подлежат. Порядок сбора страховых взносов на обязательное медицинское страхование разрабатывается Правительством РФ и утверждается высшим законодательным органом. Федеральный и территориальный фонды ОМС освобождаются от уплаты налогов по доходам от основной деятельности. Территориальные фонды финансируют страховые медицинские организации, расположенные на соответствующей территории, в которых для обеспечения стабильности страховой деятельности могут создаваться резервные фонды. Страховые медицинские организации обязаны осуществлять деятельность по обязательному медицинскому страхованию на некоммерческой основе. На страховые медицинские организации распространяется действующее на территории РФ законодательство по налогообложению.

2. Методы оценки достоверности относительных и средних величин.

Как уже отмечалось, под выборочным методом в статистике понимается такой метод наблюдения, при котором для определения типичных черт какой-либо совокупности изучаются не все единицы этой совокупности, а лишь их часть. Как бы тщательно ни производилась выборка, какой бы репрезентативной ни была выборочная совокупность (отобранная часть наблюдений), она неизбежно будет отличаться от всей генеральной (общей, исчерпывающей) совокупности. Таким образом, полного тождества результатов достичь не удается, и неизбежно остается некоторая неточность. Однако в нашем распоряжении имеются методы установления степени различий числовых характеристик обеих совокупностей и пределов возможных колебаний показателей при данном числе наблюдений. Как будет видно из последующего, значительную роль играет число наблюдений: чем больше число наблюдений, тем точнее отображается генеральная совокупность и тем меньше ошибка. Так называемые средние ошибки являются мерой точности и достоверности любых статистических величин. Теория выборочного метода, наряду с обеспечением репрезентативности, практически сводится к оценке расхождений между числовыми характеристиками генеральной и выборочной совокупности, т. е. к определению средних ошибок и так называемых доверительных границ или интервалов. Средняя ошибка позволяет установить тот интервал, в котором заключено действительное значение производной величины при данном числе наблюдений, т. е. средняя ошибка всегда является конкретной. На размеры средней ошибки влияет не только число наблюдений, но и степень колеблемости, изменчивости признаков. Чем изменчивее изучаемое явление, тем больше будет его ошибка. Это видно из формулы, по которой определяется средняя ошибка средней величины, обозначаемая буквой m. Она вычисляется, по формуле:

, где

n — число наблюдений. Между размерами сигмы (отражающей колеблемость явления) и размерами средней ошибки существует прямая связь. Между числом наблюдений и размерами средней ошибки существует обратная связь (пропорциональная не числу наблюдений, а квадратному корню из этого числа). Если вычислить среднюю ошибку для вариационного ряда, приведенного в табл. 9, где М = 62,0; N = 36; = 1,8, то получим:

.

6.1 Оценка достоверности относительных величин и различий между ними

Для оценки достоверности относительных величин необходимо определить ошибку соответствующего показателя, которая является мерой отличия выборочной совокупности от генеральной, а также свидетельствует о пределе возможных колебаний коэффициента при повторном исследовании. Ошибка относительных величин определяется по формуле:

, где

m — ошибка показателя p — шансы за (показатель) q — шансы против q = 100 – P, если показатель вычислен на 100; q = 1000 – Р, если показатель вычислен на 1000; q = 10000 – Р, если показатель вычислен на 10000; n — число наблюдений. Использование данной формулы и последовательность оценки достоверности входящих в нее величин рассмотрим на следующем примере. Так в хирургическом отделении объединенной больницы за год было прооперировано 384 человека. У 64 больных в послеоперационном периоде возникли осложнения. Требуется найти частоту возникновения осложнений, провести оценку достоверности показателя, определить его доверительные границы и достаточность объема наблюдений выборки, рассматривая последнюю как вариант пробного исследования. Решение. В данном случае необходимо вычислить интенсивный показатель Р. Примем его за x:

384 — 64 100 — х .

Затем вычисляется его ошибка (m):

.

После чего следует рассчитать величину, называемую критерием (t): 

, где

Р — относительный показатель; m — ошибка показателя Р.

.

Необходимо также задать доверительную вероятность или доверительный уровень (1 – ). Доверительный уровень показывает вероятность того, что наша оценка ошибочна, и измеряемое значение показателя не попадает в интервал Pm. Так если 1 – = 0,01, это значит, что вероятность ошибки составляет 1% (соответственно вероятность правильности оценки составляет 0,99). Показатель следует считать статистически достоверным, если коэффициент t будет превышать стандартное значение tst (коэффициент Стьюдента), приведенное в оценочной табл. 1 приложения для заданного доверительного уровня. Для определения стандартного значения необходимо найти число степеней свободы по формуле f = n – 1, где f — число степеней свободы, n — число наблюдений. f = 384 – 1 = 383. Коэффициент t = 4,6. Он превышает стандартные значения 1,96 

(1 — < 0,05), 2,58 (1 — < 0,01) и 3,29 (1 — < 0,001).

Следовательно, найденный показатель распространенности послеоперационных осложнений в хирургическом отделении является статистически достоверным более чем в 99,9%

(1 — < 0,001).

Определение доверительных границ статистического показателя осуществляется с использованием следующей формулы:

Р tm, где

Р — показатель, t — доверительный коэффициент, m — ошибка показателя. Если t = 1, то с вероятностью в 68,3% результаты выборочного исследования могут быть перенесены на генеральную совокупность. При t = 2 вероятность перенесения результатов выборочного исследования на генеральную совокупность увеличивается до 95,5%. И при t = 3 увеличивается до 99,7%. В рассмотренном примере показатель равен 16,7 на 100 обследованных, его ошибка соответствует 3,6. Для обозначения доверительных границ показателя принимается следующая запись: 16,73,6. Предельная ошибка выборочного исследования = tm позволяет определить величину доверительного интервала, в пределах которого с определенной вероятностью находится подлинный показатель генеральной совокупности. Оценка достоверности показателей выборочной совокупности должна проводиться на достаточном числе наблюдений. Необходимое число наблюдений для выборочного исследования можно определить при помощи преобразования выше приведенной формулы предельной ошибки выборки ():

, где

t — доверительный коэффициент, P — показатель, n — число наблюдений. Решая приведенное равенство относительно n, получим формулу для определения необходимого числа наблюдений:

.

Используя данные рассматриваемого примера и вычисленные на этих данных показатели, проведем проверку достаточности числа наблюдений выборочной совокупности. t — доверительный коэффициент, который при = 95,5% равен 2. Р = 16,7.  = 5% (задает сам исследователь). Тогда число наблюдений:

.

Следовательно, необходимое число наблюдений выборочной совокупности равно 222. Одним из вариантов определения объема совокупности выборочного исследования является использование специальных таблиц (см. табл. 2 приложения).

6.2 Оценка достоверности различий между относительными величинами

При определении различия между статистическими показателями расчет t-критерия производится по формуле:

, где

P1 и Р2 — сопоставляемые коэффициенты; m1 и m2 — ошибки коэффициентов Р1 и Р2. Методику оценки достоверности различий относительных величин рассмотрим на примере (цифры условные). Пример. В районе А с численностью населения 75000 за год умерло 743 человека. В районе Б, численность населения которого составила 89000, умерло 820 человек. Возрастно-половой состав проживающих в двух районах был примерно одинаковым. Требуется определить, отличаются ли уровни смертности в названных районах. Решение. 1. Определение уровня смертности (интенсивный показатель) для района А:

75000 — 743 1000 — Х %0.

Уровень смертности в районе А составил 9,9 на 1000 населения. 2. Оценка достоверности показателя смертности (район А).

.

tst = 1,96 (при 1 – =0,05); 2,58 (при 1 – = 0,01); 3,29 (при 1 – = 0,001) (см. табл. 1 приложения).

f = n – 1 = 74999.

Показатель является статистически достоверным: (1 – < 0,001). 3. Определение уровня смертности для района Б.

8900 — 820 1000 — Х .

Уровень смертности в районе Б составил 9,2 на 1000 населения. 4. Оценка достоверности показателя смертности (район Б).

.

tst = 1,96 (при 1 – =0,05); 2,58 (при 1 – = 0,01); 3,29 (при 1 – = 0,001) (см. табл. 1 приложения).

f = n – 1 = 87999.

Показатель является статистически достоверным: (1 – < 0,001). 5. Расчет t-критерия:

.

6. Оценка достоверности различий показателей смертности между районами А и Б:

f = n1 + n2 – 2; f = 75000 + 89000 – 2 = 163998; tst = 1,96 – 2,58 – 3,29 t = 0,1 < 1,96 < 2,58 < 3,29.

Следовательно, показатели смертности в двух районах статистически не отличаются ( < 95%). Если при вычислении относительных показателей на 100 величина показателя менее 20 или более 80, то ошибка относительной величины вычисляется по формуле

.

А оценка достоверности показателей соответственно по формуле

, где

M1 и M2 — частота явления в расчете на единицу наблюдения. Оценка t-критерия проводится по таблице критических значений (см. табл. 1 приложения).

6.3 Оценка достоверности средних величин и различий между ними

При оценке достоверности средних арифметических величин фактическое значение t-критерия вычисляется с использованием формулы:

, где

М — средняя величина, m — ошибка средней величины. Среднюю величину следует считать статистически достоверной, если коэффициент достоверности будет превышать стандартное значение оценочной табл. 1 (см. приложение). Методику оценки достоверности средних величин целесообразно рассмотреть на примере. Пример. При определении средней величины окружности груди у 48 восьмилетних мальчиков были получены следующие данные: M = 58,69 см, среднеквадратическое отклонения = 1,83 см и ошибка средней величины m = 0,26 см. На основании имеющихся данных необходимо провести оценку достоверности средней величины. 1. Оценка достоверности проводится с использованием вышеприведенной формулы:

.

Для определения стандартного значения необходимо найти число степеней свободы по формуле: f = n – 1 , где f — число степеней свободы, n — число наблюдений, f = 48 – 1 = 47. Коэффициент t = 225,73 превышает стандартные значения 1,98  (1 – < 0,05); 2,62 (1 – < 0,01) и 3,37 (1 – < 0,001). Следовательно, найденная средняя величина окружности груди у восьмилетних мальчиков является статистически достоверной с вероятностью > 99,9% (1 – < 0,001). 2. Определение доверительных границ средней величины следует проводить по формуле: М tm, где М — средняя величина, t —коэффициент Стьюдента, m — ошибка показателя. Если t = 1, то с вероятностью 68,3% результаты выборочного исследования могут быть перенесены на генеральную совокупность; При t = 2 вероятность переноса результатов выборочного исследования на генеральную совокупность возрастает до 95,5% и при t = 3 — до 99,7%. В рассмотренном примере средняя величина равна 58,69 см, ее ошибка соответствует 0,26 см. Для обозначения доверительных границ средней величины применима следующая запись: 58,69 0,26. Предельная ошибка выборочного исследования = tm позволяет определить величину доверительного интервала, в пределах которого с определенной вероятностью находится подлинная средняя величина генеральной совокупности. 3. Оценка достоверности средних величин выборочной совокупности должна проводиться на достаточном объеме наблюдений. Необходимое число наблюдений для выборочного исследования можно определить при помощи преобразования выше приведенной формулы предельной ошибки выборки ():

, где

t — доверительный коэффициент, m — ошибка средней арифметической, — среднеквадратическое отклонение, n — число наблюдений. Решая приведенное равенство относительно n, получим формулу для определения необходимого числа наблюдений:

.

Используя данные рассмотренного примера, проведем проверку достаточности объема наблюдений выборочной совокупности. t — доверительный коэффициент. При Р = 95,5% он равен 2. составила 1.83 см. = 0,5 см (задает сам исследователь).

.

Cледовательно, необходимый объем наблюдений выборочной совокупности равен 53.

3. По данным годового отчета (ф.30) рассчитайте и проанализируйте следующие показатели деятельности стоматологической поликлиники:

- показатель удельного веса врачей, имеющих высшую квалификационную категорию;

- показатель удельного веса врачей, имеющих первую квалификационную категорию;

- показатель удельного веса врачей, имеющих вторую квалификационную категорию.

Число врачей - физических лиц	52
Число врачей, имеющих высшую категорию	14
Число врачей, имеющих первую категорию	12
Число врачей, имеющих вторую категорию	10

4. Служащий И. , находясь в другом городе в командировке, 2.02.2010 г. заболел острым герпетическим стоматитом и был нетрудоспособен 12 дней. Лечился амбулаторно в поликлинике. Оформить нетрудоспособность.

Зав. кафедрой ОЗиЗ, проф., д.м.н. А.В. Калиниченко

Государственное образовательное учреждение

высшего профессионального образования

«Новосибирский государственный медицинский университет Федерального агентства по здравоохранению и социальному развитию»

(ГОУ ВПО НГМУ Росздрава)

Факультет: стоматологический

Кафедра: общественное здоровье и здравоохранение

Дисциплина: общественное здравоохранение и здоровье

ЭКЗАМЕНАЦИОННЫЙ БИЛЕТ № 8

1. Медицинская демография: определение, характеристика основных разделов демографии.

Демо­графия - это наука о населении. В круг проблем демографии входят изучение территориального размещения населения, тен­денций и процессов, связанных с социально-экономическими условиями жизни, быта, традициями, экологическими, медицинскими, правовыми и другими факто­рами.

Медицинская демография - изучает взаимосвязь воспроизводства населения с социально-гигиеническими факторами и разрабатывает медико-социальные меры, направленные на обеспечение наиболее благоприятного развития демографических процессов и улучшения здоровья населения.

Медицинская демография. Она изучает человеческие популяции во взаимо-

связи с биологическими, социально – экономическим, климато – географиче-

скими, экологическими и другими факторами, которые оказывают прямое

влияние на формирование и воспроизводство здоровья населения.

Медицинская демография – это отрасль знания, возникшая на стыке социаль-

ной гигиены и демографии, изучающая демографические закономерности с

точки зрения качественной характеристики народонаселения, его здоровья

(трудоспособности, длительности жизни).

Медицинская демография изучает закономерности и социально-

гигиеническую обусловленность рождаемости, физического развития, заболе-

ваемости, инвалидности, смертности, воспроизводства населения во взаимо-

связи с демографическим факторами, такими как семейное состояние населе-

ния, его миграционная подвижность, региональные особенности расселения,

демографическая структура, условия и образ жизни, демографическое поведе-

ние и др.

Наиболее актуальными направлениями в области медико-демографических

исследований на современном этапе являются:

1. Оценка количественных и качественных аспектов воспроизводства насе-

ления, разработка рекомендаций, направленных на улучшение медико-

демографической ситуации в региональном разрезе.

2. Изучение динамики состояния здоровья населения (физического развития,

заболеваемости, инвалидности, общей и младенческой смертности), факторов,

определяющих их уровней и характер.

3. Изучение влияния отдельных заболеваний на состояние здоровья разных

демографических групп населения и величину ожидаемой продолжительности

жизни.

4. Изучение тенденций в медико-демографических процессах на региональ-

ном уровне, и факторов, их обуславливающих.

5. Вопросы перспективного планирования здравоохранения на основе углуб-

ленного анализа медико-демографических процессов.

6. Определение показателей здоровья населения, на которые может повлиять

система мер по линии здравоохранения и тех показателей, которые зависят от

влияния других факторов.

7. Анализ влияния состояния здоровья женщин на их репродуктивную функ-

цию.

8. Изучение внутрисемейных аспектов регулирования рождаемости, влияние

факторов такого регулирования на здоровье населения и рождаемость.

9. Исследование процесса старения населения и проблем демографической

специализации медицинской помощи.

2. Понятие о методе корреляции, его оценка.

Корреляция – это взаимосвязь между признаками. Виды корреляционной связи: 1. Функциональная - когда любому значению одного из признаков соответствует значение другого (определенному радиусу круга соответствует определенная площадь). Такая связь характерна для физико-химических явлений.  2. Корреляционная это вид проявления количественной связи между признаками. Она характерна для медико-биологических и социально-гигиенических исследований. Возникает тогда, когда значению средней величины одного признака соответствуют несколько значений другого взаимосвязанного с ним признака (рост и масса, уровень гемоглобина и насыщенность крови кислородом). Корреляционную связь можно представить с помощью таблицы, графика.  Практическое значение:  -Для выявления причинно-следственных связей между факторными и результативными признаками (оценка физического развития, определения связи между условиями труда и состоянием здоровья).  -Зависимость параллельных изменений нескольких признаков от какой-то величины (при воздействии 1 факторного признака изменились значения нескольких результативных признаков).  Коэффициент корреляции - Это числовое значение, которое дает представление о направлении и силе связи. По направлению корреляционная связь может быть: Прямая, когда с увеличением значения одного признака увеличивается значение другого (рост-вес). Коэффициент корреляции со знаком (+). Обратная, при которой увеличение значения одного признака ведет к уменьшению значения другого (иммунитет человека и активность патогенных микроорганизмов). Коэффициент корреляции со знаком (-). Размер связи колеблется от 0 до 1: Коэффициент корреляции = 1 – полная связь. Коэффициент корреляции = 0 – отсутствие связи.  Сила связи: 1. сильная, 2. средняя, 3. слабая Методы определения коэффициента корреляции: 1. Ранговый (Спирмена). 2. Квадратов (Пирсона).

КОРРЕЛЯЦИОННЫЙ АНАЛИЗ

При изучении общественного здоровья и здравоохранения в научных и практических целях исследователю часто приходится проводить статистический анализ связей между факторными и результативными признаками статистический совокупности (причинно-следственная связь) или определение зависимости параллельных изменений нескольких признаков этой совокупности от какой либо третьей величины (от общей их причины). Необходимо уметь изучать особенности этой связи, определять ее размеры и направление, а также оценивать ее достоверность. Для этого используются методы корреляции.

1. Виды проявления количественных связей между признаками

   • функциональная связь

   • корреляционная связь

2. Определения функциональной и корреляционной связи

Функциональная связь — такой вид соотношения между двумя признаками, когда каждому значению одного из них соответствует строго определенное значение другого (площадь круга зависит от радиуса круга и т.д.). Функциональная связь характерна для физико-математических процессов.

Корреляционная связь — такая связь, при которой каждому определенному значению одного признака соответствует несколько значений другого взаимосвязанного с ним признака (связь между ростом и массой тела человека; связь между температурой тела и частотой пульса и др.). Корреляционная связь характерна для медико-биологических процессов.

3. Практическое значение установления корреляционной связи. Выявление причинно-следственной между факторными и результативными признаками (при оценке физического развития, для определения связи между условиями труда, быта и состоянием здоровья, при определении зависимости частоты случаев болезни от возраста, стажа, наличия производственных вредностей и др.)

Зависимость параллельных изменений нескольких признаков от какой-то третьей величины. Например, под воздействием высокой температуры в цехе происходят изменения кровяного давления, вязкости крови, частоты пульса и др.

4. Величина, характеризующая направление и силу связи между признаками. Коэффициент корреляции, который одним числом дает представление о направлении и силе связи между признаками (явлениями), пределы его колебаний от 0 до ± 1

5. Способы представления корреляционной связи

   • график (диаграмма рассеяния)

   • коэффициент корреляции

6. Направление корреляционной связи

   • прямая

   • oбратная

7. Сила корреляционной связи

   • сильная: ±0,7 до ±1

   • средняя: ±0,3 до ±0,699

   • слабая: 0 до ±0,299

8. Методы определения коэффициента корреляции и формулы

   • метод квадратов (метод Пирсона)

   • ранговый метод (метод Спирмена)

9. Методические требования к использованию коэффициента корреляции

   • измерение связи возможно только в качественно однородных совокупностях (например, измерение связи между ростом и весом в совокупностях, однородных по полу и возрасту)

   • расчет может производиться с использованием абсолютных или производных величин

   • для вычисления коэффициента корреляции используются не сгруппированные вариационные ряды (это требование применяется только при вычислении коэффициента корреляции по методу квадратов)

   • число наблюдений менее 30

10. Рекомендации по применению метода ранговой корреляции (метод Спирмена)

    • когда нет необходимости в точном установлении силы связи, а достаточно ориентировочных данных

    • когда признаки представлены не только количественными, но и атрибутивными значениями

    • когда ряды распределения признаков имеют открытые варианты (например, стаж работы до 1 года и др.)

11. Рекомендации к применению метода квадратов (метод Пирсона)

    • когда требуется точное установление силы связи между признаками

    • когда признаки имеют только количественное выражение

12. Методика и порядок вычисления коэффициента корреляции

1) Метод квадратов

• построить вариационные ряды для каждого из сопоставляемых признаков, обозначив первый и второй ряд чисел соответственно х и у;

• определить для каждого вариационного ряда средние значения (М₁ и М₂);

• найти отклонения (d_х и d_y) каждого числового значения от среднего значения своего вариационного ряда;

• полученные отклонения перемножить (d_x X d_y)

• каждое отклонение возвести в квадрат и суммировать по каждому ряду (Σ d_x² и d_y² )

• подставить полученные значения в формулу расчета коэффициента корреляции: 

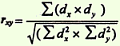
при наличии вычислительной техники расчет производится по формуле: 

2) Ранговый метод

• составить два ряда из парных сопоставляемых признаков, обозначив первый и второй ряд соответственно х и у. При этом представить первый ряд признака в убывающем или возрастающем порядке, а числовые значения второго ряда расположить напротив тех значений первого ряда, которым они соответствуют

• величину признака в каждом из сравниваемых рядов заменить порядковым номером (рангом). Рангами, или номерами, обозначают места показателей (значения) первого и второго рядов. При этом числовым значениям второго признака ранги должны присваиваться в том же порядке, какой был принят при раздаче их величинам первого признака. При одинаковых величинах признака в ряду ранги следует определять как среднее число из суммы порядковых номеров этих величин

• определить разность рангов между х и у (d): d = х — у

• возвести полученную разность рангов в квадрат (d²)

• получить сумму квадратов разности (Σ d²) и подставить полученные значения в формулу: 

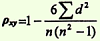
Схема оценки корреляционной связи по коэффициенту корреляции

Сила связи	Направление связи
	прямая (+)	обратная (-)
Сильная	от + 1 до +0,7	от - 1 до - 0,7
Средняя	от + 0,699 до + 0,3	от - 0,699 до - 0,3
Слабая	от + 0,299 до 0	от - 0,299 до 0