12. Необходимые и достаточные условия равновесия системы пар сил лежащих в одной плоскости.
Плоская система сил – система сил, расположенных в одной плоскости. Система сил приводится к одной силе – главному вектору и к паре сил, момент которой равен главному моменту.
Теорема Вариньона ( теорема о моменте равнодействующей силы): момент равнодействующей относительно любой точки = геометрической сумме моментов составляющих сил относительно той же точки. Условия равновесия пространств. сист.сил:
Fkx=0;
Fky=0;
Fkz=0;
Mx(Fk)=0;
My(Fk)=0;
Mz(Fk)=0.
Условия
равновесия для системы параллельных
сил (||z):
Fkz=0;
Mx(Fk)=0;
My(Fk)=0.
Центр параллельных сил – точка, через
которую проходит линия действия
равнодействующей системы ||-ых сил при
любых поворотах этих сил около их точек
приложения в одну и ту же сторону и на
один и тот же угол. Координаты центра
||-ых сил:
и т.д.
Условия
равновесия пл. сист. сил: векторное:
.
аналитич:
,
или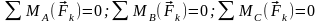
где А,В,С – точки,
не лежащие на одной прямой, или
,
ось "х" не перпендикулярна отрезку
АВ.
13.Приведение системы сил к заданному центру.
Основная теорема статики (Пуансо).
Любую произвольную систему сил, действующую на твердое тело, можно в общем случае привести к силе и паре сил. Этот процесс замены системы сил одной силой и одной парой сил называется приведением системы сил к заданному центру.
14. Главный вектор и главный момент плоской системы сил.
Главным
вектором системы сил называется вектор,
равный векторной сумме этих сил.
Главным
моментом системы сил относительно точки
О тела, называется вектор, равный
векторной сумме моментов всех сил
системы относительно этой точки.
15. Необходимые и достаточные условия равновесия плоской системы сил. Уравнения, выражающие эти условия.
На тело действует плоская система сил. Расположим оси Ox и Oy в плоскости действия сил.
Уравнения
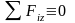
Для
равновесия плоской системы сил,
действующих на твердое тело, необходимо
и достаточно, чтобы суммы проекций этих
сил на каждую из двух прямоугольных
осей координат, расположенных в плоскости
действия сил, были равны нулю и сумма
моментов этих сил относительно любой
точки, находящейся в плоскости действия
сил также была равна нулю.
16. Момент силы относительно точки в плоской системе сил.
Момент силы лучше считать относит. точки. в которой пересек. как можно больше неизвестных сил.
17.Лемма о переносе силы в любую точку пространства.
Силу, приложенную к физ. объекту можно перенести параллельно самой себе в любую точку тела, добавив при этом момент данной силы относительно нового центра ее приложения. Пусть на А действует сила F, возьмем произвольную т. В и приложим к ней уравновешенную систему сил {F1,F2} такую, что F1=F2=F . Состояние тела Bне меняется.F1,F2- пара сил и ее момент: M{F1,F2}=-F*a=-F*h= . Т.о., сила F,приложенная к т.А перенесена параллельно самой себе в произвольную точку тела B,но при этом к телу добавлен ее момент относительно точки В.
18. Простейшие виды плоской системы сил, Приведение к равнодействующей, к паре сил. Приведение к паре
Пусть
в результате приведения сил к центру О
оказалось, что главный вектор равен
нулю, а главный момент отличен от нуля:
. Тогда в силу основной теоремы статики
можем написать
Это означает, что исходная система сил в этом случае эквивалентна паре сил с моментом .
Приведение к равнодействующей
Пусть теперь главный вектор не равен нулю, а главный момент равен нулю: . В силу основной теоремы статики имеем
то есть система сил оказывается эквивалентной одной силе - главному вектору. Следовательно, в этом случае исходная система сил приводится к равнодействующей, и эта равнодействующая совпадает с главным вектором, приложенным в центре приведения: . Система сил приводится к равнодействующей и в том случае, когда главный вектор и главный момент оба не равны нулю, но взаимно перпендикулярны: . Доказательство осуществляется при помощи следующей последовательности действий.