62. Электромагнитные волны. Вектор Умова-Пойнтинга.
Колебания,которые распространяются в пространстве-волны. Волны – это изменение состояния среды или возмущения, распространяющиеся в этой среде и несущие с собой энергию.
Наиболее часто встречающиеся виды волн – упругие, поверхностные, электромагнитные.
1. Существуют электромагнитные волны, то есть распространяющееся в пространстве и во времени электромагнитное поле. Электромагнитные волны поперечны – векторы Е и В перпендикулярны друг другу и лежат в плоскости, перпендикулярной направлению распространения волны .
2.
Электромагнитные волны распространяются
в веществе с конечной скоростью
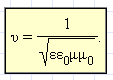
Скорость
электромагнитных волн в вакууме (ε = μ
= 1):
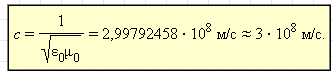
3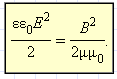
.
В электромагнитной волне происходят
взаимные превращения электрического
и магнитного полей. Эти процессы идут
одновременно, и электрическое и магнитное
поля выступают как равноправные
«партнеры».
4.Электромагнитные волны переносят энергию. При распространении волн возникает поток электромагнитной энергии. Если выделить площадку S (рис. 2.6.3), ориентированную перпендикулярно направлению распространения волны, то за малое время Δt через площадку протечет энергия ΔWэм, равная ΔWэм = (wэ + wм)υSΔt.
Электромагнитная волна может переносить электромагнитную энергию (поток энергии). Вычислим поток электромагнитной энергии в вакууме, исходя из уравнений Максвелла. Для этого умножим обе стороны уравнения (12.1) скалярно на Е , а обе стороны уравнения (12.2) – на Н :
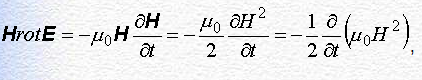(1)
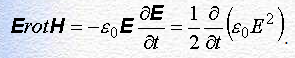(2)
Используем формулу векторного анализа
и, соответственно, вычтем из уравнения (1)выражение (2)
Введем обозначение:
где S называют вектором Умова–Пойнтинга. Этот вектор определяет направление распространения энергии волны.
Запишем теперь окончательное выражение для вектора Умова–Пойнтинга в плоской волне:
Полученное равенство имеет простой смысл. Через единичную площадку, поставленную перпендикулярно распространению волны, в единицу времени проходит энергия, заключенная в цилиндре с площадью основания, равной единице, и высотой .
.
63. Энергия электромагнитного поля.
64. Взаимодействие электромагнитного поля с вещество
