58. Волновое уравнение.

59. Интерференция и дифракция волн. Принцип Гюйгенса- Френеля.

60. Электромагнитные колебания. Колебательный контур.

61. Электромагнитное поле. Уравнения Максвелла.

62. Электромагнитные волны. Вектор Умова-Пойнтинга.

63. Энергия электромагнитного поля.

64. Взаимодействие электромагнитного поля с вещество

59. Интерференция и дифракция волн. Принцип Гюйгенса- Френеля.

Явление дифракции объясняется с помощью принципа Гюйгенса, согласно которому каждая точка, до которой доходит волна, служит центром вторичных волн, а огибающая этих волн задает положение волнового фронта в следующий момент времени. Принцип Гюйгенса решает лишь задачу о направлении распространения волнового фронта, но не затрагивает вопроса об амплитуде и интенсивности волн, распространяющихся по разным направлениям.

Френель вложил в принцип Гюйгенса физический смысл, дополнив его идеей интерференции вторичных волн.

При рассмотрении дифракции Френель исходил из нескольких основных положений, принимаемых без доказательства. Совокупность этих утверждений и называется принципом Гюйгенса–Френеля.

Согласно принципу Гюйгенса, каждую точку фронта волны можно рассматривать как источник вторичных волн.

Френель существенно развил этот принцип.

• Все вторичные источники фронта волны, исходящей из одного источника, когерентны между собой.

• Равные по площади участки волновой поверхности излучают равные интенсивности (мощности).

• Каждый вторичный источник излучает свет преимущественно в направлении внешней нормали к волновой поверхности в этой точке. Амплитуда вторичных волн в направлении, составляющем угол α с нормалью, тем меньше, чем больше угол α, и равна нулю при .

• Для вторичных источников справедлив принцип суперпозиции: излучение одних участков волновой поверхности не влияет на излучение других (если часть волновой поверхности прикрыть непрозрачным экраном, вторичные волны будут излучаться открытыми участками так, как если бы экрана не было).

58. Волновое уравнение.

Пусть в момент времени t₁ = 0 в точке с координатой х возникло некоторое возмущение  всплеск на воде, удар барабана, переменное электрическое поле и т.д., способное распространяться вдоль оси х вправо со скоростью v.

Форма этого возмущения описывается функцией f(x₁), где f(x₁) может быть смещением точки из положения равновесия, отклонением давления от среднего значения, напряженностью электрического или магнитного поля и т.д.

Если возмущение распространяется без искажений со скоростью v вправо, то функция f должна таким образом зависеть от х и t, чтобы выполнялись соотношения

f(x₁,t₁) = f(x₂,t₂)

 возмущение переходит из точки x₁, t₁ в точку x₂, t₂, не меняя формы, где

x₂ = x₁ + v(t₂  t₁) ,

о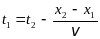 ткуда

x₁ = x₂  v (t₂  t₁),

Если возмущение распространяется вправо, то функция f зависит лишь от комбинации аргументов x и t

f = f₁(x  vt).

Действительно, одному значению аргумента

a = x  vt соответствует одно значение функции f(a). Положение координаты х = а + vt этого возмущения распространяется вправо со скоростью

Если возмущение движется влево, то оно описывается уравнением

f = f₂(x + vt), поскольку из условия, что одинаковому значению аргумента а соответствуют равные значения функции, следует f(x + vt) = f(a). Координата этого возмущения смещается влево x = a  t со скоростью V.

Р аспространение возмущения в пространстве можно описать при помощи дифференциального уравнения.

В одномерном случае

Этому уравнению удовлетворяют функции

f₁(x  vt), f₂(x + vt) и их суперпозиция f₁(x  vt) + f₂(x + vt).

Полученное уравнение называется волновым уравнением.