13. Дать определение сходящейся числовой последовательности. Сформулировать арифметические действия со сходящимися числовыми последовательностями. Доказать одно из перечисленных свойств.
Последовательность, имеющая предел, называется сходящейся; в противном случае – расходящейся.
Сумма двух сходящихся последовательностей и есть сходящаяся последовательность, предел которой равен сумме пределов последовательностей u.
Доказательство: Пусть а и b – соответственно пределы последовательностей {хn} и {yn}. Тогда:
xn=а+a n, yn=b+b n,
где {a n} и {b n) – бесконечно малые последовательности. Следовательно, (хn + yn) - (а + b) =a n+b n.
Таким образом, последовательность {(хn + yn) - (а + b)} бесконечно малая, и поэтому последователдьность {хn + yn} сходится и имеет своим пределом число а+b. Теорема доказана.
Разность двух сходящихся последовательностей и есть сходящаяся последовательность, предел которой равен разности пределов последовательностей u.
Произведение двух сходящихся последовательностей и есть сходящаяся последовательность, предел которой равен произведению пределов последовательностей u.
14. Доказать теорему о предельном переходе в неравенствах для числовых последовательностей.
Теорема. Если элементы сходящейся последовательности {xn}, начиная с некоторого номера, удовлетворяют неравенству xn ≥ b (xn ≤ b), то и предел a этой последовательности удовлетворяет неравенству a ≥ b (a ≤ b).
Доказательство. Пусть все элементы xn, по крайней мере начиная с некоторого номера, удовлетворяют неравенству xn ≥ b. Требуется доказать неравенство a ≥ b. Предположим, что a < b. Поскольку a - предел последовательности {xn}, то для положительного ε = b - a можно указать номер N такой, что при n ≥ N выполняется неравенство |xn - a| < b - a. Это неравенство эквивалентно следующим двум неравенствам: -(b - a) < xn - a < b - a. Используя правое из этих неравенств, получим xn < b, а это противоречит условию теоремы. Случай xn ≤ b рассматривается аналогично. Теорема доказана.
15. Доказать второй замечательный предел и вывести следствия из доказанного предела.
или 
Доказательство второго замечательного предела:
Доказательство для натуральных значений
Докажем
вначале теорему для случая
последовательности 
По
формуле бинома
Ньютона: 
Полагая 
,
получим:
(1)
Из
данного равенства (1) следует, что с
увеличением n число положительных
слагаемых в правой части увеличивается.
Кроме того, при увеличении n число 
убывает,
поэтому величины 
возрастают.
Поэтому последовательность 
— возрастающая,
при этом
(2).
Покажем, что она ограничена. Заменим каждую скобку в правой части равенства на единицу, правая часть увеличится, получим неравенство
Усилим полученное неравенство, заменим 3,4,5, …, стоящие в знаменателях дробей, числом 2:
.
Сумму в скобке найдём по формуле суммы членов геометрической прогрессии:
.
Поэтому 
(3).
Итак,
последовательность ограничена сверху,
при этом 
выполняются
неравенства (2) и (3): 
.
Следовательно,
на основании теоремы Вейерштрасса
(критерий сходимости последовательности)
последовательность 
монотонно
возрастает и ограниченна, значит имеет
предел, обозначаемый буквой e.
Т.е. 
Зная,
что второй замечательный предел верен
для натуральных значений x, докажем
второй замечательный предел для
вещественных x, то есть докажем, что 
.
Рассмотрим два случая:
1.
Пусть 
.
Каждое значение x заключено между двумя
положительными целыми числами: 
,
где 
—
это целая часть x.
Отсюда
следует: 
,
поэтому
.
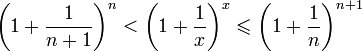Если
,
то 
.
Поэтому, согласно пределу
,
имеем:
.
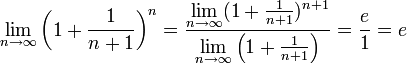
По
признаку (о пределе промежуточной
функции) существования пределов 
.
2.
Пусть 
.
Сделаем подстановку 
,
тогда
.
Из двух этих случаев вытекает, что для вещественного x.