1. Дать определение действительного числа. Рассказать о геометрической иллюстрации действительного числа.

Множество действительных чисел (R) содержит рациональные и иррациональные числа. Всякое рациональное число выражается или конечной десятичной дробью

или бесконечной периодической дробью. Так, 1/2 = 0,5 (= 0,500 ... ), 1/3 = 0,333 ... - рациональные числа.

Действительные числа, не являющиеся рациональными, называются иррациональными.

2. Дать определение числового множества. Привести примеры числовых множеств. Дать определение окрестностей точки.

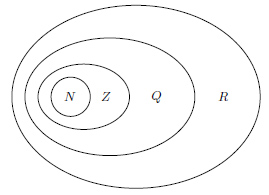
Множества, элементами которых являются числа, называются числовыми. Примерами числовых множеств являются:

N = {1; 2; 3; ... ; n; ... } - множество натуральных чисел;

Z = {О; ±1; ±2; ... ; ±n; ... } - множество целых чисел;

Q = {m/n m Е Z, n Е N} - множество рациональных чисел.

R - множество действительных чисел.

Пусть а и b - действительные числа, причем а < b.

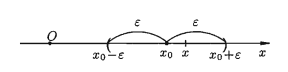
Пусть хо - любое действительное число (точка на числовой пря-

мой). Окрестностью точки хо называется любой интервал (а; b),

содержащий точку хо. В частности, интервал (хо - е, хо + е), где е > 0,

называется e - окрестностью точки хо. Число хо называется центром, а число е - радиу-сом.

3. Рассказать об операциях над множествами. Привести примеры.

Объединением (суммой) множеств А и В называется множество А ∪ В, элементы которого принадлежат хотя бы одному из этих множеств.

Например, если А={1,2,4}, B={3,4,5,6}, то А ∪ B = {1,2,3,4,5,6}

Пересечением (произведением) множеств А и В называется множество А ∩ В, элементы которого принадлежат как множеству А, так и множеству В.

Например, если А={1,2,4}, B={3,4,5,2}, то А ∩ В = {2,4}

Разностью множеств А и В называется множество АВ, элементы которого принадлежат множесву А, но не принадлежат множеству В.

Например, если А={1,2,3,4}, B={3,4,5}, то АВ = {1,2}

Симметричной разностью множеств А и В называется множество А Δ В, являющееся объединением разностей множеств АВ и ВА, то есть А Δ В = (АВ) ∪ (ВА).

Например, если А={1,2,3,4}, B={3,4,5,6}, то А Δ В = {1,2} ∪ {5,6} = {1,2,5,6}

4. Дать определения функции; обратной функции; сложной функции. Рассказать о нахождении обратной функции для функции y = sin x.

Функция — математическое понятие, отражающее связь между элементами множеств. Можно сказать, что функция — это «закон», по которому каждому элементу одного множества x (называемому областью определения) ставится в соответствие некоторый элемент другого множества y (называемого областью значений).

Пусть задана функция у = f(x) с областью определения D и множеством значений Е. Если каждому значению у Е E соответствует единственное значение х Е D, то определена функция х = f(у) с областью определения Е и множеством значений D (см. рис. 102). Такая функция f(у) называется обратной к функции f(x) и записывается в следующем виде: х = f ^–1 (y). Про функции У = f(x) и х = f ^–1 (У) говорят, что они являются взаимно обратными. Чтобы найти функцию х = f ^–1 (у), обратную к функции у = f(x), достаточно решить уравнение f(x) = у относительно х (если это возможно).

Сложная функция, функция от функции. Если величина y является функцией от u, то есть у = f (u), а и, в свою очередь, функцией от х, то есть u = f(х), то у является С. ф. от х, то есть y = f [(x)], определённой для тех значений х, для которых значения f(х) входят в множество определения функции f (u). В таком случае говорят, что у является С. ф. независимого аргумента х, а u — промежуточным аргументом.