Лекции по математическому анализу_1 / Лекция 38

Лекция 38 . Поверхностные интегралы.

П.1 Поверхности в пространстве. Площадь поверхности.

ОПР. Гладкая поверхность в пространстве задается параметрическими уравнениями

в векторной форме , , где - замкнутая измеримая область на плоскости переменных (u,v) , или в координатной форме с заданными функциями имеющие непрерывные частные производные первого порядка в .

Пусть ступенчатая фигура , вписанная в , состоящая из квадратов пересекающихся только по граничным точкам.

Параметр ступенчатой фигуры . Через обозначим площадь двух треугольников в пространстве с вершинами в точках и , где - образы вершин квадрата : при отображении . Тогда и . Площадь треугольника равна . Аналогично, и , а площадь треугольника равна

. Тогда =.Здесь производные и вычисляются в точке . Величина = представляет собой площадь

кусочно-плоской поверхности составленной из треугольников, вписанной в .

ОПР. Площадью поверхности называют число =.

ТЕОРЕМА 1 (формула для вычисления площади поверхности )

Если поверхность задается уравнениями с непрерывно дифференцируемыми функциями то площадь поверхности существует и равна

= (1)

ДОК. Величина =, где , а

- бесконечно малая функция при . В условиях теоремы величина , представляя собой интегральную сумму для (1) , имеет

предел, равный правой части формулы (1). Тогда при имеет тот же предел, поскольку они отличаются на .

УПРАЖНЕНИЕ. Доказать, что для поверхности с уравнением , ,

где имеет непрерывные частные производные по обеим переменным о точках области , ее площадь поверхности вычисляется по формуле :

(2)

ДОКАЗАТЕЛЬСТВО. Перепишем уравнение поверхности в параметрической форме :

. Тогда и , а их векторное произведение равно

. Длина = и формула (2) следует из (1) после возврата к переменным x и y .

ПРИМЕР 1. Вычислить площадь шарового сегмента сферы радиуса R и высотой h .

: , .

РЕШЕНИЕ. Перепишем уравнение поверхности в параметрической форме, используя сферические координаты : , .

, ,

, .

Тогда .

П.2 Поверхностный интеграл первого рода.

ОПР. Окрестностью поверхности называют множество точек в пространстве ,

являющихся внутренними хотя бы для одного шара радиуса с центром в точке поверхности .

Рассматривается скалярная функция непрерывная в окрестности

кусочно-гладкой поверхности , заданной параметрическими уравнениями.

Пусть - ступенчатая фигура соответствующая разбиению области на прямоугольники , , пересекающиеся только в граничных точках. Через обозначим образ прямоугольника при отображении . По предположению имеет площадь, которую обозначим . Пусть , , набор произвольных точек .

ОПР. Интегральной суммой функции по поверхности называют величину

.

ОПР. Поверхностным интегралом первого рода функции по поверхности

называют величину

. (2)

СВОЙСТВА ПОВЕРХНОСТНОГО ИНТЕГРАЛА первого рода.

1. линейность : .

2. аддитивность по множеству : если и , - два куска имеющих площадь и пересекающихся только по граничным точкам, то .

3. оценка интеграла : если и , то справедлива оценка

.

4. теорема о среднем для поверхностного интеграла : в предположении непрерывности функции существует точка , для которой .

ТЕОРЕМА 2. Если функция непрерывная в окрестности

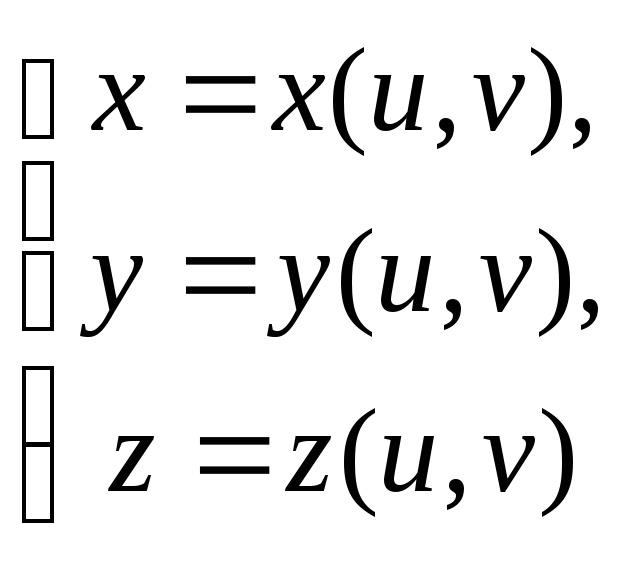
кусочно-гладкой поверхности , заданной параметрическими уравнениями , то поверхностный интеграл первого рода существует и вычисляется по формуле :

(3)

ДОК. Интегральная сумма для двойного интеграла (3) равна

.

Поверхностный интеграл (3) с учетом теоремы о среднем можно представить в виде :

.

Величина представляет собой интегральную сумму для площади поверхности и имеет по условию теоремы предел при равный ,т.е. она ограничена некоторой константой .

Оценим абсолютное значение разности :

,

где - колебание функции . С учетом непрерывности функция бесконечно малая в точке и для любого существует такое, что для всех разбиений области с параметром выполняется неравенство :

, что доказывает утверждение теоремы.

ЗАМЕЧАНИЕ . Если поверхность задается явно, т.е. с помощью уравнения ,

, то поверхностный интеграл вычисляется по формуле :

(4)

ПРИМЕР 2. Вычислить интеграл , где - граница тела .

РЕШЕНИЕ. Коническая поверхность , , , ==.

Поверхность круга , , .

Тогда =.

П.3 Поверхностные интегралы второго рода.

Рассмотрим векторно-значную функцию ,

непрерывную в окрестности кусочно-гладкой поверхности , задаваемую уравнениями .

ОПР. Полем нормалей гладкой поверхности называют совокупность векторов , , перпендикулярных касательным плоскостям к поверхности в точках М и непрерывно зависящих от М . Поверхность вместе с фиксированным полем нормалей называют ориентированной.

ОПР. Поверхность называют двусторонней , если обход по любому замкнутому контуру, лежащему на поверхности и не имеющему общих точек с ее границей, не меняет направления поля нормалей. В противном, поверхность называется односторонней.

Сторона двусторонней поверхности определяется фиксацией поля нормалей.

Если поверхность ограничивает тело в пространстве, то поле нормалей, указывающее направление внутрь тела, задает ее внутреннюю сторону поверхности, а противоположное поле нормалей – внешнюю сторону. Иногда сторону поверхности с нормалями , составляющими острый угол с положительным направлением оси OZ, называют верхней, а противоположную – нижней.

Если границей гладкой поверхности является контур , то направление обхода контура нужно согласовать с выбранным полем направлений, т.е. со стороной поверхности : из конца вектора для и близких к движение по контуру должно происходит против часовой стрелки.

Если поверхность кусочно-гладкая и контур разделяет два ее соседних куска и

, то направления поля нормалей на них должно быть согласовано : направление обхода контура , согласованное с полем , , противоположно направлению

обхода , согласованного с полем ,.

ОПР. Если фиксирована сторона кусочно-гладкой двусторонней поверхности , т.е. фиксировано согласованное поле направлений по кускам ее составляющим, то поверхностным интегралом второго рода функции по ориентированной поверхности называется величина, обозначаемая , равная

=, (5)

где = - единичный вектор поля нормалей.

Если поверхность ориентирована противоположным образом, то интеграл меняет знак.

Интеграл (5) представляет собой поверхностный интеграл первого рода для скалярной функции и способ его вычисления определяется формулой :

= (6)

ЗАМЕЧАНИЕ. Если поверхность задается явно уравнением ,,

выбрана верхняя ее сторона : , то

=.

Интеграл по нижней стороне поверхности отличается знаком.

ПРИМЕР 3. Вычислить интеграл , где - внешняя сторона сферы : .

РЕШЕНИЕ. Внешняя нормаль =, функция =,

скалярное произведение =. Тогда

==.

ВОПРОСЫ К ЭКЗАМЕНУ.

1. Поверхность в пространстве, способы ее задания. Площадь поверхности и способ

ее вычисления.

2. Поверхностный интеграл первого рода, его свойства. Формула вычисления интеграла.

3. Ориентированная поверхность. Поверхностный интеграл второго рода.

Формула вычисления интеграла.