Лекции по математическому анализу_1 / Лекция 36

Лекция 36. Тройной интеграл.

П.1 Измеримые множества в пространстве. Понятие тройного интеграла.

«Кирпичиком» для построения измеримых множеств в пространстве является параллелепипед с вершиной в точке , его параметр - диагональ параллелепипеда.

ОПР. Телом в пространстве называют открытую, односвязную и ограниченную область в . Замкнутая область – это , где - совокупность граничных точек .

ОПР. Ступенчатым телом называют объединение параллелепипедов , возможно пересекающихся по границе, =. Ступенчатое тело вписано в , если , и описано, если . Параметром ступенчатого тела называют число =.

ОПР. Нижней мерой тела называется число , где верхняя грань берется по всем ступенчатым телам, вписанным в . Верхняя мера тела называется число , где - ступенчатые тела описанные около . Числа и существуют для любой .

ОПР. Тело измеримо в пространстве , если ==.

Число называется мерой тела или его объемом.

ПРИМЕРЫ измеримых областей.

1. для любой вершины , .

2. - прямой цилиндр, образующая которого перпендикулярна плоскости ХОУ, с основанием и высотой , , где - площадь области .

ПОЯСНЕНИЕ. Если ступенчатая область вписанная в , то объединение параллелепипедов является ступенчатым телом, вписанным в . Его объем при стремится к величине .

3. - стандартная область по оси ОZ,

где кусочно-гладкие функции в измеримой области на плоскости .

.

ПОЯСНЕНИЕ. Если ступенчатая область вписанная в и , , то объединение параллелепипедов представляет ступенчатое тело вписанное в , а объединение параллелепипедов - ступенчатое тело описанное около . Предел объемов каждого из них при

равен .

4. Тело с измеримыми сечениями. Рассматриваются тела , у которых сечения плоскостями перпендикулярными координатным осям , например, плоскостями с уравнением , измеримы на плоскости ХОУ, т.е. для любого область измерима и ее мера непрерывная функция переменной на отрезке [a,b]. Множество назовем сечением тела плоскостью . Тогда тело и ее объем.

ПОЯСНЕНИЕ. Если разбиение отрезка [a;b] , то ( мера симметрической разности)есть бесконечно малая функция параметра разбиения . Разбиение пересечения на прямоугольники = порождает разбиение тела на параллелепипеды . Объем ступенчатого тела построенного из них равен , где при , и стремится к при уменьшении параметра разбиения.

В частности, цилиндр 2) тело с измеримыми сечениями и - постоянная на отрезке функция.

ПРИМЕР 1. Найти объем тела ограниченного поверхностями : , , ,

, .

РЕШЕНИЕ. Рассмотрим сечения плоскостями .Тогда область ( трапеция) на плоскости имеет границы , , , и ее мера (площадь)

- непрерывная функция

на отрезке [0;1]. Тогда объем тела равен :

.

П.2 Тройной интеграл.

Пусть - измеримое тело и =соответствующее разбиение на параллелепипеды . В каждом параллелепипеде выберем произвольную точку .

ОПР. Интегральной суммой функции по области называют выражение :

.

ОПР. Тройным интегралом Римана функции по области называют число :

.

Если функция имеет тройной интеграл, то она называется интегрируемой по Риману в области .

ТЕОРЕМА 1. (необходимое условие интегрируемости)

Если функция интегрируема в измеримой области , то она ограничена в .

ДОК. ( аналогично соответствующей теореме для двойного интеграла)

ТЕОРЕМА 2. ( достаточное условие интегрируемости)

Всякая кусочно-непрерывная на измеримом множестве функция интегрируема по Риману .

ДОК. ( аналогично соответствующей теореме для двойного интеграла)

СВОЙСТВА ТРОЙНОГО ИНТЕГРАЛА. ( аналогичны свойствам двойного интеграла).

1. линейность : .

2. аддитивность по множеству : , где и - измеримые множества пересекающиеся по границе. Тогда .

3. теорема о среднем : Если непрерывна на , то существует точка

, для которой .

4. Оценка отклонения интеграла от интегральной суммы :

,

где - любое разбиение на параллелепипеды с параметром , а - функция колебания :=. Для непрерывной функции на колебание бесконечно малая функция в точке .

5. Если = характеристическая функция области , то

.

П.3 Повторные интегралы.

Вычисление тройного интеграла сводится к вычислению двойных и одномерных интегралов, т.е. к повторному интегрированию. Для областей рассмотренных выше эта процедура следующая (рассматриваются функции кусочно-непрерывные в ).

1. Если =, то .

Внутренний одномерный интеграл берется по переменной z на отрезке , при фиксированных x и y , и поэтому является непрерывной функцией двух переменных .

Интегрирование этой функции по переменной y на отрезке при фиксированном x задает функцию переменной x , которая интегрируется на отрезке

. Порядок интегрирования может быть изменен.

2. Если =, то .

Внутренний двойной интеграл берется по области на плоскости ХОУ при фиксированном z и является непрерывной функцией этой переменной , которая интегрируется на отрезке [a,b] .

3. Если =, то .

Внутренний одномерный интеграл берется по переменной z при фиксированных

на отрезке и является непрерывной функцией этих переменных. Последняя функция интегрируется по области , и полученное число представляет тройной интеграл функции по области .

4. Если =, то .

Внутренний двойной интеграл берется по сечению области плоскостью , а внешний одномерный интеграл берется по отрезку значений параметра p , при которых

эти сечения не пусты.

ДОКАЗАТЕЛЬСТВО. Проведем его в случае, когда функция непрерывна в .

(изменения, связанные с кусочной непрерывностью функции , подробно обсуждались при повторном интегрировании в двойных интегралах). Например, представим интеграл 4.

в виде интегральной суммы функции по области . Разобьем отрезок [a;b] точками . Тогда по свойствам одномерного интеграла существует набор точек , для которых

=. Разобьем область на измеримые части , для которых величина ) достаточно мала. Тогда по теореме о среднем для двойного интеграла существуют точки , для которых

=)= =. Последнее представляет собой интегральную сумму функции по области , разбитую на цилиндры , диаметры которых как угодно малы. Тогда

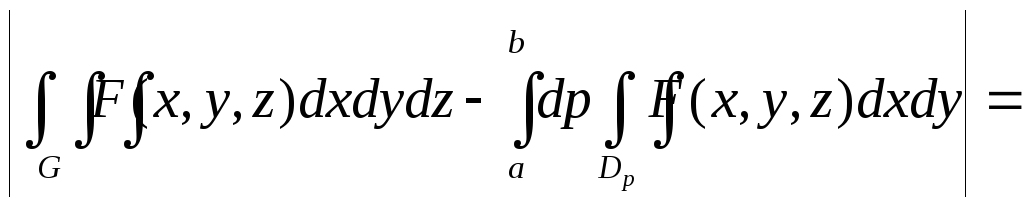
= для любого . Последнее доказывает формулу 4.

ПРИМЕР 2. Вычислить интеграл , где область ограничена поверхностями :

, , , ,, .

РЕШЕНИЕ. Буква z наиболее часто встречается в уравнениях границы, поэтому сечения следует проводить перпендикулярно оси OZ плоскостями . Сечением являются прямоугольники , границы которого имеют уравнения : , , , ,

. Тогда =.

П.3 Замена переменной в тройном интеграле.

ОПР. Заменой переменной в пространстве называют биективное отображение области в на область в , при котором каждая точка переходит в точку , причем .

Отображение задается непрерывно дифференцируемыми функциями , , .

Определитель называется якобианом отображения .

ПРИМЕР 3 (сферическая замена переменных)

Положение точки в пространстве можно характеризовать тремя числами , , - сферическими координатами точки. Здесь - расстояние точки до точки О - начала координат, . Если проекция точки на плоскость ХОУ , то - угол, который образует вектор с положительным направлением оси ОХ, . Наконец, - угол, который образует вектор с плоскостью ХОУ, .Связь между декартовыми и сферическими координатами осуществляется по формулам :

. Например, прообразом шара : при отображении сферической замены является параллелепипед .

Якобиан сферической замены

=

ЗАМЕЧАНИЕ.

Иногда в сферической замене вместо угла используют угол , , образуемый вектором с положительным направлением оси OZ. В этом случае соответствующая замена переменных задается формулами : ,

а якобиан .

ПРИМЕР 4. (Цилиндрическая замена )

Положение точки в пространстве можно характеризовать тремя числами

и называемыми цилиндрическими координатами точки . Здесь - длина вектора

на плоскости ХОУ, , - угол, который образует вектор с положительным направлением оси ОХ, , и - проекция вектора на ось OZ, .

Связь между декартовыми и цилиндрическими координатами осуществляется по формулам :.

УПРАЖНЕНИЕ. Вычислить якобиан цилиндрической замены переменных.

Ответ : . Прообразом прямого кругового цилиндра при отображении цилиндрической замены является параллелепипед .