Лекции по математическому анализу_1 / Лекция 39
.docЛекция 39. Элементы теории поля.
П.1 Формула Грина.
Рассмотрим область
на плоскости
,
которую возможно задать двумя способами
:
и
.
Пусть
векторнозначная функция, для которой
имеют непрерывные частные производные
в
.
Граница
области
предполагается кусочно-гладкой и
ориентированной так, что при ее обходе
область
остается слева. Такое направление обхода называют положительным.
Тогда криволинейный интеграл
=
=
=
.
Аналогично, криволинейный интеграл
=
=
.
Тогда
.
Если область
,
причем
и
из
этого объединения могут пересекаться
только по границам
и
, то
на кривой
,
состоящей из внутренних точек области
,
ориентации
и
противоположны и криволинейные интегралы
по отличаются только знаком.
Через
обозначим набор
.
Тогда
+
=
=
+
=
+
+
+
.
В последних двух суммах каждое слагаемое
встречается дважды, один
раз со знаком плюс , а другой со знаком минус, поскольку это интегралы по контурам
типа
.
Итак, доказана формула Грина
=
, (1)
связывающая криволинейные интегралы по границам областей на плоскости с двойными интегралами по этим областям.
УПРАЖНЕНИЕ. Докажите, что площадь области
,
ограниченной замкнутой кривой
,
можно вычислять по
формуле :
.
ДОК. Применим формулу Грина :
.
ПРИМЕР 1. Вычислить площадь области,
ограниченной кривой :
.
РЕШЕНИЕ. Воспользуемся обобщенными
полярными координатами :
Подставляем их в уравнение границы :
- полярное уравнение кривой. Перейдем
к параметрическим уравнениям :
и
.
Тогда
.
=
.
П.2 Формула Стокса.
Пусть
- кусок гладкой двусторонней ориентированной
поверхности с границей
,
направление обхода которой согласовано
с выбором стороны поверхности, т.е.
фиксацией непрерывного поля нормалей.
Будем полагать , что поверхность
можно
задать явно каждым из трех уравнений :
а)
,
, б)
,
,
в)
с непрерывно дифференцируемыми функциями
.
Через
обозначим границу области
.
Направление обхода
и
согласовано с выбором поля нормалей
=
.
Пусть задано непрерывно дифференцируемое
поле
в
окрестности
.
Тогда а)
=
формула
Грина = =
=
=
.
Аналогично, устанавливаются соотношения
: б)
,
в)
.
Складывая полученные выражения, получим
.
ОПР. Поле
называется ротором поля
.
Если
- формальный вектор (оператор
дифференцирования) , то
можно
представить в форме векторного
произведения
и
:
=
.
Доказанную формулу для гладкого куска
можно
записать в форме
.
Если поверхность
есть объединение гладких кусков ,
пересекающихся только по своим границам
, то ориентация поверхности
выбирается так, что направление обхода
контуров
в кусках
и
противоположное и значения криволинейных
интегралов на них противоположно по
знаку. Обозначим через
набор
,
где
-
согласованно ориентированная граница
поверхности
.
Тогда
=
+
+
.
Слагаемые в последних двух суммах входят парами, одно со знаком плюс , а другое, равное ему по абсолютному значению, со знаком минус, поэтому суммы равны нулю.
Итак, доказана формула Стокса :
=
(2)
ПРИМЕР 2. Вычислить криволинейный
интеграл
,
где
контур, направление обхода по которому
против часовой стрелки,
если смотреть с положительной полуоси ОХ.
РЕШЕНИЕ. Поверхность
- плоскость
,
с согласованным полем нормалей
.
.
.
.
Тогда
=
.
П.3 Формула Остроградского.
Пусть
область в пространстве
с кусочно-гладкой границей
.Поверхность
ориентирована внешним по отношению к
полем
нормалей. Пусть задано непрерывно
дифференцируемое в
поле
.
ОПР. Дивергенцией поля
называют скалярную функцию :
.
Пусть
область с границей
,
уравнение которой можно задать явно
каждым из трех уравнений : а)
,
,
,
, б)
,
,
,
,в)
с непрерывно дифференцируемыми функциями
и кусочно-гладкими
границами областей
,
и
.
Например, область
=
.
Тогда
=
=
+
=
.
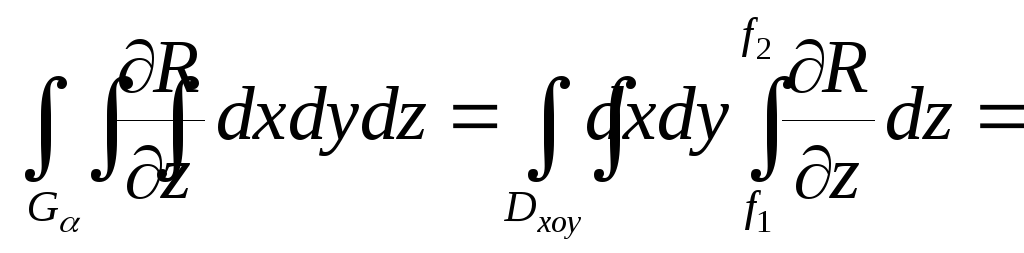
Аналогично, доказываются соотношения
:
,
.
Складывая интегралы в левых частях
равенств,
получим
.
Полагаем, что область
разбита на конечное число областей типа
:
=
пересекающихся только по границам
,
причем ориентация кусков
в областях
и
противоположная и поэтому потоки поля
через них компенсируют друг друга. Пусть
набор областей
,
для которых
.
Тогда
+
+
=
=
+
+
.
Слагаемые в первой и второй суммах компенсируют друг друга в силу противоположных
ориентаций общих кусков границы, поэтому суммы равны нулю. Итак, доказана
формула Остроградского :
=
(3).
УПРАЖНЕНИЕ. Доказать, что объем тела
,
ограниченного кусочно-гладкой поверхностью
,
можно вычислить по формуле :
,
где
- внешняя нормаль.
ДОК.
,
,
далее формула (3).
ПРИМЕР. 3 Вычислить интеграл
,
где
- поверхность единичного куба
.
РЕШЕНИЕ.
,
.
По формуле (3)
=2
=2
=
=
.
П.4 Дифференциальные операторы.
А. Оператор =
.
Через формальный вектор , скалярное и векторное произведение можно представить
градиент скалярной функции
,
дивергенцию и ротор векторного поля
:
=
=
,
(4)
=
=
,
(5)
=
(6)
Действие оператора
, где
- векторное поле, на скалярную функцию
и векторную функцию
осуществляется по формулам :
(
)
(7)
(
)
=
(8)
Свойства оператора .
1. линейность.
,
(9)
,
(10)
,
(11)
2. Действие на произведение :
,
(12)
,
(13)
,
(14)
,
(15)
,
(16)
,
(17)
(18)
Б. Оператор Лапласа
=
.
Действие оператора Лапласа на скалярную
функцию
и векторную
осуществляется так :
,
Оператор Лапласа линеен :
(19)
Свойства операций второго порядка :
,
(20)
,
(21)
,
(22)
,
(23)
.
(24)
ВОПРОСЫ К ЭКЗАМЕНУ.
1. формула Грина.
2. Формула Стокса.
3. Формула Остроградского.
4. Дифференциальные операторы
и
.
Свойства операторов.
