
Лекции по математическому анализу_1 / Лекция 37
.docЛекция 37. Криволинейные интегралы.
П.1 Кривые в пространстве. Длина кривой.
ОПР. Кривая
![]() в
пространстве в векторной форме задается
уравнением
в
пространстве в векторной форме задается
уравнением
![]()
![]()
или в скалярном виде
 с заданными функциями
с заданными функциями
![]() ,
,![]() ,
,![]() .
.
(параметрическое уравнение кривой).
Кривая не имеет самопересечений, если
отображение
![]()
![]() биективно.
биективно.
Кривая называется гладкой, если функции
![]() ,
,![]() ,
,![]() непрерывно дифференцируемые
непрерывно дифференцируемые
на отрезке
![]() или кусочно-гладкой , если соответствующие
функции имеют кусочно-непрерывные
производные на отрезке
или кусочно-гладкой , если соответствующие
функции имеют кусочно-непрерывные
производные на отрезке
![]() .
.
Пусть
![]() разбиение отрезка
разбиение отрезка
![]() и
соответствующее ему разбиение кривой
и
соответствующее ему разбиение кривой
![]() точками
точками
![]() .
Через
.
Через
![]() обозначим ломаную линию, составленную
из отрезков
обозначим ломаную линию, составленную
из отрезков
![]() ,
,
![]() . Пусть
. Пусть
![]() - длина ломаной
- длина ломаной
![]() ,
т.е.
,
т.е.
![]() =
=![]()
![]() .
.
ОПР. Кривая
![]() называется
спрямляемой, если
называется
спрямляемой, если
![]() .
.
ОПР. Длиной
![]() кривой
кривой
![]() называют
число
называют
число
![]() .
.
Если кривая имеет длину, то она спрямляема.
ТЕОРЕМА 1.
Если кривая
![]() кусочно-гладкая, то она имеет длину,
вычисляемую по формуле :
кусочно-гладкая, то она имеет длину,
вычисляемую по формуле :
![]() (1)
(1)
ДОК. Докажем первоначально формулу для
гладкой кривой
![]() .
По теореме о среднем для производных
существуют точки
.
По теореме о среднем для производных
существуют точки![]() ,
для которых
,
для которых
![]() .
.
Пусть
![]() интегральная сумма для (1) , соответствующая
разбиению
интегральная сумма для (1) , соответствующая
разбиению
![]() ,
,
![]() .
.
Лемма. Справедлива оценка :
![]()
![]() ,
(2)
,
(2)
где
![]() - колебание векторнозначной функции
- колебание векторнозначной функции
![]() .
.
ДОК. По неравенству треугольника
![]()
![]()
![]() .
.
Воспользуемся результатом леммы для
оценки величины
![]() :
:
![]()
![]()
![]() .
.
Пусть
![]() произвольное число. Из непрерывности
функций
произвольное число. Из непрерывности
функций
![]() и
и
![]() следует, что функция
следует, что функция
![]() бесконечно
малая в точке
бесконечно
малая в точке
![]() .
Тогда найдется
.
Тогда найдется
![]() ,
при котором для любого разбиения
,
при котором для любого разбиения
![]() ,
,
![]() выполнено неравенство
выполнено неравенство
![]()
![]() .
.
По условию теоремы интегральные суммы
![]() имеют
предел равный
имеют
предел равный
![]() ,
поэтому
,
поэтому
![]() ,
,
т.е.длина кривой определяется формулой (1).
Если кривая
![]() кусочно-гладкая
, то она разбивается на конечное кусков
гладких кривых, длины которых вычисляются
по формуле (1) на каждом из кусков и
справедливость (1) для кусочно-гладкой
кривой следует из свойства аддитивности
интеграла по множеству.
кусочно-гладкая
, то она разбивается на конечное кусков
гладких кривых, длины которых вычисляются
по формуле (1) на каждом из кусков и
справедливость (1) для кусочно-гладкой
кривой следует из свойства аддитивности
интеграла по множеству.
УПРАЖНЕНИЕ. Докажите, что если кривая
![]() на
плоскости задается графиком непрерывно
дифференцируемой функции
на
плоскости задается графиком непрерывно
дифференцируемой функции
![]() на отрезке [a;b],
то длина кривой вычисляется по формуле
:
на отрезке [a;b],
то длина кривой вычисляется по формуле
:
![]() (3)
(3)
ДОК. Уравнение кривой можно записать в
параметрической форме :
 ,
,
![]() .
.
Тогда
![]() и
формула (1) переходит в (3).
и
формула (1) переходит в (3).
П.2 Криволинейные интегралы первого рода.
ОПР. Окрестностью
![]() кривой
кривой
![]() назовем
множество точек М пространства, для
которых найдется шар радиуса
назовем
множество точек М пространства, для
которых найдется шар радиуса
![]() с центром в точке кривой
с центром в точке кривой
![]() такой,
что М является его внутренней точкой.
такой,
что М является его внутренней точкой.
Рассмотрим непрерывную скалярную
функцию
![]() ,
определенную в окрестности
,
определенную в окрестности
![]() кусочно-гладкой
кривой
кусочно-гладкой
кривой
![]() .
Каждому разбиению
.
Каждому разбиению
![]()
отрезка [a,b]
и набору точек
![]() соответствует
число
соответствует
число
![]()
=![]() ,
,
называемое интегральной суммой функции
![]() по кривой
по кривой
![]() .
.
ОПР. Криволинейным интегралом первого
рода функции
![]() по кривой
по кривой
![]() называют
называют
число
![]()
![]() (4)
(4)
ТЕОРЕМА 2.(необходимое условие существования криволинейного интеграла)
Если функция
![]() имеет криволинейный интеграл первого
рода , то она ограничена на множестве
точек кривой.
имеет криволинейный интеграл первого
рода , то она ограничена на множестве
точек кривой.
ДОК. (без доказательства)
ТЕОРЕМА 3. Если функция
![]() непрерывна
в окрестности
непрерывна
в окрестности
![]() кусочно-гладкой
кривой
кусочно-гладкой
кривой
![]() ,
то она имеет криволинейный интеграл
первого рода по этой кривой.
,
то она имеет криволинейный интеграл
первого рода по этой кривой.
ДОК. ( без доказательства)
ЗАМЕЧАНИЕ. Условие непрерывности функции
![]() можно понизить до ее кусочной непрерывности
.
можно понизить до ее кусочной непрерывности
.
СВОЙСТВА криволинейного интеграла.
1. линейность
![]() .
.
2. аддитивность по кривой. Если кривая
![]() состоит
из двух, не имеющих общих точек, кроме
граничных, кусков
состоит
из двух, не имеющих общих точек, кроме
граничных, кусков
![]() и
и
![]() , т.е.
, т.е.
![]() ,
то
,
то
![]() .
.
3. Если
![]() в точках кривой
в точках кривой
![]() ,
то
,
то
![]() .
.
4. (оценка интеграла) Если
![]() и
и
![]() ,
то
,
то
![]() .
.
5. (теорема о среднем для криволинейного
интеграла) Существует точка
![]() ,
для которой
,
для которой
![]() .
.
ТЕОРЕМА 4. ( Формула для вычисления криволинейного интеграла первого рода)
Если функция
![]() непрерывна в окрестности
непрерывна в окрестности
![]() кусочно-гладкой кривой
кусочно-гладкой кривой
![]() ,
заданной параметрическими уравнениями
:
,
заданной параметрическими уравнениями
:

![]() ,
то
,
то
![]()
![]() (5)
(5)
ДОК. Пусть
![]() разбиение отрезка [a;b]
и
разбиение отрезка [a;b]
и
![]() первоначально
гладкая кривая. Интегральная сумма для
криволинейного интеграла имеет вид :
первоначально
гладкая кривая. Интегральная сумма для
криволинейного интеграла имеет вид :
![]()
![]() ,
(6)
,
(6)
где
![]() .
Интегральная сумма
.
Интегральная сумма
![]() для
интеграла в правой части (5) имеет
для
интеграла в правой части (5) имеет
вид :
![]()
![]() .
Для оценки абсолютного значения разности
.
Для оценки абсолютного значения разности
![]() воспользуемся результатами леммы (2) :
воспользуемся результатами леммы (2) :
![]()
![]()
![]() .
.
Тогда
![]()
![]() ,
,
где
![]() .
Если кривая
.
Если кривая
![]() гладкая,
то для любого
гладкая,
то для любого
![]() существует
существует
![]() ,
для которого
,
для которого
![]() и
и
![]()
![]() .
.
По условиям теоремы интегральные суммы
![]() имеют предел при
имеют предел при
![]() ,
поэтому неравенство справедливо после
предельного перехода :
,
поэтому неравенство справедливо после
предельного перехода :
![]() ,
,
а , следовательно, существует предел
при
![]() последовательности
последовательности
![]() интегральных сумм криволинейного
интеграла равный (5).
интегральных сумм криволинейного
интеграла равный (5).
Если кривая
![]() кусочно-гладкая, то она представляет
объединение конечного числа гладких
кусков, для каждого из которых справедлива
формула (5) и общий результат следует из
свойства аддитивности по кривой
криволинейного интеграла.
кусочно-гладкая, то она представляет
объединение конечного числа гладких
кусков, для каждого из которых справедлива
формула (5) и общий результат следует из
свойства аддитивности по кривой
криволинейного интеграла.
ПРИМЕР 2. Вычислить
![]() , где
, где
![]() .
.
РЕШЕНИЕ. Запишем параметрические
уравнения кривой
![]() ,
используя полярные координаты :
,
используя полярные координаты :
![]() ,
,
![]() .
.
Тогда
![]() и
и
![]() =
=![]()
П.3 Криволинейный интеграл второго рода.
Рассмотрим векторно-значную функцию
![]() непрерывную в некоторой окрестности
непрерывную в некоторой окрестности
![]() кусочно-гладкой
кривой
кусочно-гладкой
кривой
![]() .
Для каждого разбиения
.
Для каждого разбиения
![]() отрезка [a;b]
и любого набора точек
отрезка [a;b]
и любого набора точек
![]() определим
число
определим
число
![]() -
сумму по k скалярных
произведений векторов
-
сумму по k скалярных
произведений векторов
![]() и
и
![]() .
В координатной форме
.
В координатной форме
![]() имеет вид :
имеет вид :
![]() =
=![]()
![]() ,
,
где
![]() ,
и называется интегральной суммой поля
,
и называется интегральной суммой поля
![]() по кривой
по кривой
![]() .
.
ОПР. Криволинейным интегралом второго
рода векторного поля
![]() по кривой
по кривой
![]() ,
,
обозначение
![]() , называют число
, называют число
![]() =
=![]() (7)
(7)
ТЕОРЕМА 5. ( теорема существования)
Если поле
![]() непрерывно в окрестности
непрерывно в окрестности
![]() кусочно-гладкой
кривой
кусочно-гладкой
кривой
![]() ,
то криволинейный интеграл второго рода
существует.
,
то криволинейный интеграл второго рода
существует.
ДОК. (Без доказательства)
ТЕОРЕМА 6. ( формула вычисления криволинейного интеграла второго рода)
Если поле
![]() непрерывно в окрестности
непрерывно в окрестности
![]() кусочно-гладкой
кривой
кусочно-гладкой
кривой
![]() :
:
![]() ,
то
,
то
![]() =
=![]() (8)
(8)
ДОК. Предположим первоначально, что
кривая
![]() гладкая.
Пусть
гладкая.
Пусть
![]() разбиение отрезка [a;b]
.По теореме о среднем для производной
существует набор точек
разбиение отрезка [a;b]
.По теореме о среднем для производной
существует набор точек
![]() ,
для которых
,
для которых
![]() =
=![]()
![]() .
.
Интегральная сумма
![]() для интеграла в правой части (8) имеет
вид :
для интеграла в правой части (8) имеет
вид :
![]() =
=![]()
![]() .
.
Если
![]() ,
то
,
то
![]()
![]() .
.
Если кривая
![]() гладкая, то для любого
гладкая, то для любого
![]() существует
существует
![]() ,
для которого
,
для которого
![]() и
и
![]() для любых разбиений
для любых разбиений
![]() ,
,
![]() .
.
По условию теоремы интегральные суммы
![]() имеют предел при
имеют предел при
![]() ,
поэтому
,
поэтому
![]()
![]()
![]() ,
,
т.е. справедлива формула (8).
Если кривая
![]() кусочно-гладкая, то она представляет
собой объединение конечного числа
гладких кусков, для которых справедлива
формула (8) и результат следует из свойства
аддитивности интеграла по множеству.
кусочно-гладкая, то она представляет
собой объединение конечного числа
гладких кусков, для которых справедлива
формула (8) и результат следует из свойства
аддитивности интеграла по множеству.
ЗАМЕЧАНИЕ. Утверждение теоремы остается справедливым для кусочно-непрерывных
векторных полей
![]() в окрестности кривой
в окрестности кривой
![]() .
.
ПРИМЕР. Вычислить
![]() ,
где
,
где
![]() .
.
РЕШЕНИЕ. Напишем параметрические
уравнения окружности
![]() ,
используя сферические координаты :
,
используя сферические координаты :
![]()
![]() ,
,
![]()
![]() .
Тогда
.
Тогда
 ,
,
![]() и
и
![]() =
=
=![]()
=![]() .
.
УСЛОВИЯ НЕЗАВИСИМОСТИ криволинейного интеграла от пути .
ОПР. Поле
![]() определенное в области
определенное в области
![]() называется потенциальным, если существует
скалярная функция
называется потенциальным, если существует
скалярная функция
![]() ,
для которой
,
для которой
![]() в каждой точке
в каждой точке
![]() .
Функция
.
Функция
![]()
называется потенциалом поля
![]() .
.
Поле
![]() потенциально в том и только в том случае,
если справедливы тождества
потенциально в том и только в том случае,
если справедливы тождества
![]() ,
,
![]() ,
,
![]() в каждой точке
в каждой точке
![]() .
(9)
.
(9)
Необходимость следует из равенства смешанных производных :
![]() .
Остальные соотношения устанавливаются
аналогично.
.
Остальные соотношения устанавливаются
аналогично.
Если (9) выполняются в открытой односвязной области , то функция

является потенциалом
![]() .
Здесь
.
Здесь
![]() фиксированная точка, С – произвольная
константа.
фиксированная точка, С – произвольная
константа.
Действительно,

=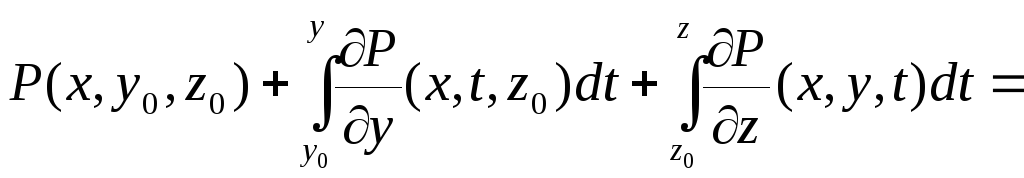 =
=![]() =
=![]() .
.

= .
.
![]() .
.
Если поле потенциально, то криволинейный
интеграл
![]() зависит только от начальной и конечной
точек кривой
зависит только от начальной и конечной
точек кривой
![]() ,
а именно,
,
а именно,
![]() =
=![]() ,
,
где
![]() ,
,
![]() .
Действительно,
.
Действительно,
![]() =
=
![]() =
=![]() .
.
СЛЕДСТВИЕ. Если поле
![]() потенциально в области
потенциально в области
![]() ,
то
,
то
![]() =0
=0
для любого замкнутой кривой
![]()
![]() .
.
ПРИМЕР Вычислить интеграл
![]() ,
где
,
где
![]() -
кривая , соединяющая точку А на
-
кривая , соединяющая точку А на
сфере
![]() и точку В на сфере
и точку В на сфере
![]() .
.
РЕШЕНИЕ. Потенциал поля равен
![]() и поэтому
и поэтому
![]() =
=![]() .
.
ВОПРОСЫ К ЭКЗАМЕНУ.
1. Кривые в пространстве. Длина кривой и способ ее вычисления.
2. Понятие криволинейного интеграла первого рода. Формула вычисления криволинейного интеграла первого рода .
3. Понятие криволинейного интеграла второго рода. Формула вычисления криволинейного интеграла второго рода.
4. Потенциальные поля, условия потенциальности. Независимость криволинейного интеграла от пути интегрирования.
