18. Определение производной; задачи, приводящие к понятию производной.

Задачи, приводящие к понятию производной

 

1. Задача о скорости движения. Рассмотрим уравнение неравномерного прямолинейного движения S=¦(t), определенного на множестве (a,b). Зафиксируем последовательно два момента времени t₀ и t ₁ Î(a,b) и обозначим  D t =t₁ - t₀.

Средней скоростью движения, соответствующей некоторому промежутку времени t, называется отношение пройденного пути, за этот промежуток времени

                                             (2-66)

Средняя скорость не характеризует движение в каждый момент времени. Для того чтобы найти скорость в данный момент t₀, необходимо уменьшить промежуток времени t=t₁-t₀. Чем меньше промежуток , тем меньше средняя скорость отличается от скорости в данный момент времени, т. е. от мгновенной, точное значение скорости   равно пределу   при , т. е.   

                                      (2-67)

2.     Задача о касательной. Пусть на множестве (a, b) задана функция y=¦(x). Отметили в декартовой ee системе координат XOY график в виде кривой К x₀;

Возьмем две точки М₀ (¦(x₀)) и М₁(x₁;¦(x₁)) и проведем через них секущую М₀ М₁, ее угол наклона обозначим через a₁. Тогда, если точка М₁, двигаясь по кривой будет приближаться к точке М₀, положение секущей изменяется.

 

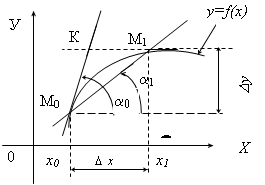
Рис. 2.17. К задаче о секущей

Когда точка М₁ совместиться с М₀, секущая превратиться в касательную. В этом случае  a₁=a₀, где a₀ - угол наклона касательной.

Из рисунка видно, что

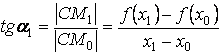                        (2-68)

т.к. x₁-x₀=D x- это приращение аргумента, ¦(x₁)-¦(x₀)=D y - приращение функции, то

tga₁=                                                       (2-69)

Осуществляя предельный переход, когда М₁ М₀

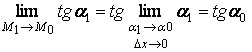.                (2-70)

Учитывая (2-69), имеем

                             (2-71)

Итак, тангенс угла наклона касательной  , равен пределу отношения приращения функции к приращению аргумента, когда последнее, равно нулю.

Тангенс угла наклона касательной показывает, во сколько раз быстрее изменяется функция по сравнению с изменением аргумента в точке касания, т.е. характеризует скорость процесса или явления, описываемого кривой К. Зная тангенсы углов наклона касательной к графику функции в двух различных точках, можно сравнивать ’’крутизну подъема’’ графика. Так в точке (x₀,f(x₀)) (см. рис.) касательная расположена ''круто'', т. е. тангенс угла наклона большой, функция изменяется быстро, тогда как в точке (x₁,f(x₁)) тангенс угла наклона касательной мал, функция изменяется медленно.

В точках, где касательная горизонта (tg =0), изменение функции почти не происходит.

Если касательная к графику функции в некоторой точке ^ к оси OX, то функция изменяется с бесконечно большой скоростью.

Определение производной

Пусть функция y=f(x) определена на некотором промежутке. При каждом значении аргумента (x) из этого промежутка функции y=f(x) имеет вполне определенное значение.

         Пусть аргумент(x) получил некоторое приращение Dх. Тогда новое значение функции будет равно f(x+Dx) т. е. новое значение функции увеличилось (изменилось) на величину

                                               (2-72)

Составим отношение приращения функции к приращению аргумента

                                             (2-73)

        Найдем предел этого отношения при    

                                (2-74)

                Определение.

             Производной функции y=f(x) точке (x) называется предел отношения приращения функции к приращению аргумента, когда последнее, стремиться к нулю, т. е. предел

                     (2-75)

Замечание:        к понятию производной мы пришли через нахождение предела отношения Dy и Dx, естественно об этом можно говорить только тогда, когда этот предел существует.

Еще замечание    производная сама тоже является функцией от (x).

Операция (действие) нахождения производной называется дифференцированием функции (о самом слове несколько попозже).